Caractéristiques de graphes

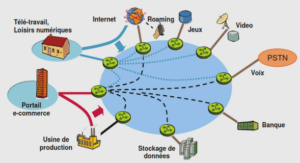
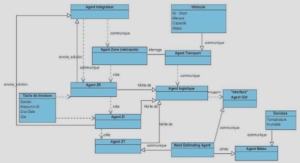
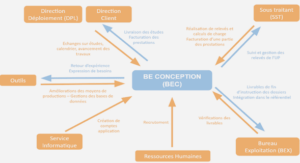
Caractéristiques de graphes

La notion de connexité est liée à l’existence de chaîne dans un graphe. Depuis un sommet, existe-t-il un une chaîne pour atteindre tout autre sommet les graphes connexes correspondant à la représentation naturelle que l’on se fait d’un graphe .Les graphes non connexes apparaissent comme la juxtaposition d’un ensemble de graphes : ses composantes connexes. Définition 1 Un graphe G = (S, A) est dit connexe pour tout couple de sommet si et sj Є S, il existe une chaîne reliant si et sj Définition 2 Un graphe G =(S, A) est dit non convexe s’il existe au moins un couple de sommets ( so1 , so2) tel que n’existe aucune chaîne joignant so1 à so2 . Exemple 1 G1 est un graphe convexe tandis que G2 n’est pas convexe car il n’existe une chaîne joignant s2 à s6 .

Graphe fortement connexe

Définition 3 Un graphe G = (S, A) est dit fortement connexe si pour tout couple de sommets si Є S et sj Є S ,il existe un chemin joignant si et sj Remarque 1 Tout graphe fortement connexe est connexe car un chemin est une chaîne . Dans GH avec H c S tel que pour tout s Є S-H le sous graphe GH U {s} n’est pas connexe . Conséquence. Dans le cas où un graphe G = (S,A) est non connexe, alors il peut être divise en p composantes connexes tels que : G = G1 U G2 U ….U Gp avec Gi ∩ Gj =ø Définition 4 On appelle degré de connexité du graphe G = (S,A) le nombre p de composantes connexes de G .Il est noté C (G).

G est un graphe connexe et C(G) =1, mais si on supprime le point s3 on aura le graphe G’ suivant qui possède deux composantes connexes G’1 et G’2 donc le point s3 est point d’articulation . 1- 4-2 Pont d’un graphe Définition 6 On appelle pont d’un graphe G un arc dont la suppression augmente la connexité du graphe . Exemple 5 L’arc (s4, s6) est un pont . En effet quand on l’élimine on augmente la connexité.

Ensemble d’articulation H ⊂ S d’un graphe connexe G

d’articulation l’ensemble H tel que le sous graphe GS-H ne soit plus connexe . Remarque 3 Les composantes connexes C1 , C2 —Cp de GS-H définissent des graphes connexes GC1UH, GC2UH, …, appelés les pièces( relativement à l’articulation H ). Proposition 1 Soit G=(S, A) un graphe connexe possédant n sommets et m arcs alors m ≥ n-1 Preuve . Raisonnons par induction . La proposition est vrai pour n = 1 car m = 0 vraie aussi pour n=2 car m = 1. Supposons pour n ≥3 la proposition vraie, pour tout graphe à n –1 sommets. Soit s le sommet de G de degré minimal de dm= d(s) alors dm ≥1 car G est connexe .Le graphe Gs =G-s possédant n-1 sommets, d’après l’hypothèse d’ induction le nombre d’arcs ms du graphe Gs est tel que ms ≥.n-1 n , donc ms donc ms ≥ n-2 . En conséquence m = ms + d (s) ≥ n-2 + d (s) ≥ n – 2 +1 = n – 1 d’ou le résultat. Proposition 2 Soit G = (S, A)un graphe non connexe possédant n sommets et m arcs si le degré de connexité C (G)= k, alors k ≥ n- m Preuve . Notons d’abord que si n ≤ m alors n-m ≤ 0 .En conséquence le degré de connexité k positif par définition vérifie k ≥ 0 ≥n – m . Supposons donc n > m Si k = 1 alors G est connexe et la proposition ci-dessus donne le résultat. Si k > 1, soit Gi, i= 1 ;2 ;3 ;…. ;k les composantes connexe de G et ni leur nombre de sommets, alors G1U G2 U……..U Gk avec n= n1 + n2 + n3+……..+ nk . Soit mi le nombre d’arcs de Gi , alors m = m1 + m2 …………+ mk .Comme chaque Gi est connexe ; alors d’après la proposition précédente mi ≥ ni-1 i = 1, 2,……….,k .En conséquence

Remarque 6 les p sommets de l’ ensemble S1 du graphe biparti complet Kp,q sont de degré q tandis que ceux de S2 sont de degré p. En effet comme chaque sommet de S1 est lié aux q autres sommets de S2 , alors il est de degré q et vice versa. Définition 11. Graphe topologique planaire Un graphe G= (S, A) est topologiquement planaire si les arcs ou arêtes de sa représentation graphique sur un plan n’intersectent qu’au niveau des sommets Définition 12 Graphe planaire Un graphe G= (S, A) est planaire s’il admet une représentation topologiquement planaire .