Hydraulic control characterization a modal Froude number

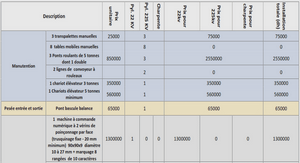
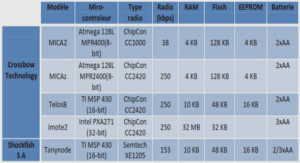
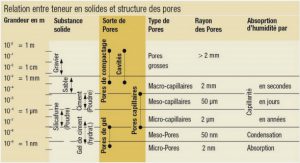
Hydraulic control characterization a modal Froude number

Hydraulic control mechanism is based on the theory of supercritical flows, which uses a parameter called the internal Froude number to characterize the hydraulic state of the flow. The Froude number is a dimensionless quantity that expresses, in this case, the ratio of the velocity of a fluid to the velocity of a linear internal wave on the interface. Some studies have adapted this strait will be discussed. Indeed, in linear theory, hydraulic control is located above the strait so above a varying topography. The modal decomposition does not apply for a varying bottom. So in controversial cases, a comparison between a modal decomposition in shallow water (at the shallowest strait depth h=D) and a modal decomposition in deep water (above the flat bottom at the maximum strait depth, h=H=0,2m) is made. In such cases, a second modal Froude number interpolated for shallow water is used: , cn,D is the mode celerity calculated at the shallowest strait depth so for a total depth of D.

Control by topography in linear regimes

A simulation, Sim0, with subcritical topography, is shown in Figure 2 (d) after 5.6 forcing periods (t=90s). The primary four plots (a,b,c) are vertical velocity analytical fields calculated according to the stratification profile (∆ρ, δρ,hρ,H) and the forcing periodicity (T) based on vertical modes decomposition approach. As the topography is subcritical, an assumption is made that the amplitudes of the vertical modes are inversely proportional to the mode number ( . In these configurations, the vertical stratification profile is not linear, so the internal wave structure is more complex. In particular, the wavenumber, kn, is no more linearly proportional to the mode number, n, even if the wavenumber still grow with the mode number. Consequently, we assume that the amplitudes of the vertical modes are rather proportional to the wavenumber .

A singular value decomposition (SVD) analysis on the vertical velocity field is used to identify the dominant vertical modes (Appendix 3). Figure 3 represents time series (b) and vertical spatial patterns (a) associated to the first three empirical orthogonal functions (EOF). Two SVD analysis at different locations in space are presented: the first location is far from the strait (x1=13.2m-plain lines) to have a long transitive time series, providing a better decorrelation of the first and second vertical mode, the other one is close to the strait (x2=11.2m) to obtain a maximum amount of information with a longer time series (dotted lines). The first two EOF modes, in both locations, have the same periodicity as the tides (b-EOF1-EOF2). The third EOF mode, EOF3, has a pseudo-periodicity of 13.5-14.5 seconds, in both locations, fitting neither tidal or harmonic periodicity (T/2,T/3…). The percentage of variance explained associated to it is very small (3% at x1, 2% at x2). The signal is quite chaotic and the vertical spatial patterns associated (a-EOF3-dashed and dotted lines) do not match to any theoretical vertical mode profile (bold lines). Vertical spatial patterns associated to EOF1 (a- EOF1- dashed-dotted line) match approximately theoretical mode 1 vertical profile (bold line). Moreover, the initial time of the perturbation (b-EOF1- dashed-dotted line) fit vertical mode 1 arrival dotted line), where mode 1 and mode 2 are temporally close and more difficult to decorrelate. Indeed, vertical modes are not strictly independent from each other. There can be different kinds of interactions between them: advection of a higher mode by a lower one resulting in non-linear effects and property changes due to varying topography or varying stratification. That’s why, there are some discrepancies between analytical vertical mode profiles (bold line-a) and EOF1 and 2 profiles (dashed and plain line-a). To conclude, SVD analysis succeeds to analyze the structure of the first two vertical modes. The percentage of variance explained associated to EOF1 (85% at x1, 84% at x2) is much higher than that of EOF2 (11% at x1, 12% at x2) indicating a domination of the first mode.

Supercritical topography

On figure 5-a-b-c-d, we can see the constructive superposition of vertical modes in the pycnocline and the apparition of the structured ray. The greater the number of modes involved, the finer the structure of the ray becomes. In figure 5-e, we can point out the contribution of each vertical mode during the transition period: the higher modes do not propagate as fast as the lower modes (as shown by the arrows). In this transition area, the first three modes are cleary distinguishable. There is a good agreement between the theoretical vertical mode structures (a,b,c,d) and the vertical velocity field in Sim1 (f). However, near the strait, where the steady state is already established, the superposition of the vertical mode and the apparition of the ray structure render more difficult the identification of each vertical mode involved. The associated density field and isopycnal vertical displacements show that the first three modes have significative amplitude, hence energy seems concentrated in these three modes. So it is difficult to determine which of these vertical modes are the most energetic but we can clearly identify the structure of the first three vertical modes on density and velocity field. Moreover, internal wave ray (IWR) angle, vertical mode wavelength and celerity in Sim1 for the first three modes correspond to theoretical values (table 3 – validation-).