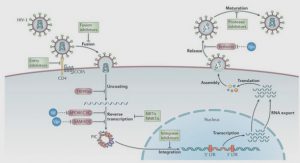
Thermométrie
But : mesurer des températures que l’on aura définies auparavant. Historiquement : avant d’avoir défini l’échelle absolue, on a seulement repéré les températures. Comme les points de repères étaient différents, les échelles de températures utilisées ça et la le furent aussi…d’où l’intérêt de ce chapitre ! 1] Equilibre thermique 1.1) Principe de l’équilibre thermique Un principe ne se démontre pas. Il est vérifié par l’expérience et est tenu pour vrai tant que rien n’est venu l’infirmer.
On considère trois systèmes A, B et C, qui ne peuvent échanger que de la chaleur à travers les cloisons qui les séparent : Si A est en équilibre thermique avec C Si B est en équilibre thermique avec C Alors A est en équilibre thermique avec B Ceci constitue le principe de l’équilibre thermique, appelé aussi principe zéro (P 0 ) de la thermodynamique. 1.2) Conséquences de P0 Il existe (sans la définir de manière rigoureuse) une grandeur commune à A , B et C appelée température. tous les systèmes qui ne sont pas en équilibre thermique n’ont pas la même température. Remarque : le temps mis pour atteindre l’équilibre ne dépend que de la nature des parois. 1.3) Utilité de l’équilibre thermique On va utiliser un thermomètre, c’est à dire un système dont un des paramètres sera relié à température (selon une loi quelconque). A l’équilibre thermique, c’est à dire lorsque ce paramètre sera stationnaire, on connaîtra la valeur de repérée.
On fera l’hypothèse que la mesure n’apporte pas de variation de au système. Exemple : on se sert d’une règle métallique en cuivre. Comme le Cu solide se dilate sous l’effet d’augmentation de température (effet toujours constaté), la longueur L de cette règle va nous donner une image de : L est dite grandeur thermométrique, et L ( ) est dite équation thermométrique. 1.4) Définitions Phase : partie homogène d’un corps délimitée par une frontière (réelle ou imaginaire) bien définie. Points fixes : états d’équilibres particuliers ou subsistent plusieurs phases. Ils sont facilement reproductibles. Exemple : équilibre eau-glace sous la pression atmosphérique de 1 atmosphère à 0° C. Remarque : Un équilibre n’est pas toujours simple à décrire, ainsi, à chaque instant, il y a autant d’eau qui se change en glace que de glace qui se change en eau..
D’autres exemples d’équilibres ont été vus en chimie en classe de terminale. Cas à connaître : Soit g la grandeur thermométrique • si g = K , un seul point fixe suffit pour déterminer la valeur de K, réel positif. On parle d’échelle de température à un point fixe. si g= a +b il faut deux points fixes, et on parle alors d’échelle à deux points fixes. 2] Echelles centésimales de température. Ce sont des échelles à deux points fixes. Par convention : Le premier point fixe, P 1 correspondra à = 0 degré de l’échelle. Le second point fixe P 2 correspondra à = 100 degrés de l’échelle. Exemple : on reprend la règle en cuivre, dont on considère la longueur, sous 1 atmosphère.
Cette règle est immergée dans de l’eau, et L ( + b. 1er point fixe : équilibre eau glace (1 atm.) : = 0 L 0 = b 2ème point fixe : eau bouillante sous 1 atm. : = 100 L 100 = +b On en déduit facilement que . Donc pour une longueur L quelconque, Il est donc possible d’associer une échelle linéaire et centésimale de température repérée, pour toute longueur comprise entre L 0 et L100 . La valeur de est donnée par : Remarques : on parle d’échelle linéaire et centésimale car on peut graduer 100 graduations régulièrement espacées sur une échelle entre celle qui correspond à L 0 et celle qui correspond à L 100 . on peut aussi ajouter des graduations avant 0 (températures repérées négatives) et des graduations au delà de la centième. Inconvénients : Si on remplace l’eau par de l’alcool, on aura encore deux points fixes, mais les deux échelles ne pourront pas être comparées : c’est l’inconvénient principal des échelles de températures repérées. Si on change de règle, une autre échelle centésimale ne va coïncider que pour les deux “ points fixes ”.
Exemple : t est repérée grâce à une règle en aluminium, puis par une règle en cuivre. Les points fixes sont les mêmes que précédemment (glace fondante et eau bouillante) et l’on suppose que t-t ’ s’annule trois fois : en 0, t1 et en 100. De plus, t’-t présente un maximum en t = 40. Ainsi, la fonction la plus simple permettant de représenter t’-t est une fonction polynôme du troisième degré en t, soit une fonction.