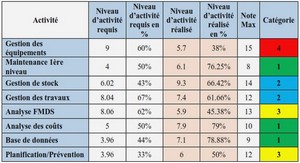
Télécharger le fichier original (Mémoire de fin d’études)
The Scanning Tunneling Microscope
The first technique to reproducibly achieve atomic-size contacts was the Scanning Tunneling Microscope (STM) with which even a controlled atomic switch has been operated [3]. Presently, the widespread technique to produce contacts with a STM works as follows. The sharp metallic tip of a STM is first pressed against a metallic surface to form through a plastic deformation a large contact. Subsequently, an elongated contact is formed as the tip is withdrawn using a piezoelectric actuator. The conductance of the contact is monitored on-flight providing an indirect information on the size of the contact. Generally speaking, a conductance of the order of the conductance quantum G0 2e 2 h 1 12.9 k1 indicates that the contact has an atomic size. This fast technique (one can pull out the tip in as short as 1ms, still slow compared to the atom dynamics), allows to perform statistical measurements of the properties of these contacts [4]. For this kind of experiments the STMs usually operate at room temperature in air, but in order to get accurate measurements of the properties of individual contacts it is better to work at cryogenic temperatures. When associated to an Atomic Force Microscope (AFM) that measures the force between the tip and the metallic surface, this technique allows to probe the internal mechanical strength and atomic rearrangements in atomic-size contacts simultaneously with conductance measurements [5,6]. In other experiments, the structure of the neck connecting the tip to the metallic surface has been directly observed with a transmission electron microscope, which allows to relate the atomic configuration to the conductance of the contact [7,8].
The Mechanical Controllable Break Junction technique (MCBJ)
This second technique used to obtain atomic size contacts was developed in 1992 by the team of J.M. van Ruitenbeek at Leiden University [9] as an extension of the “break junction technique” pioneered by Moreland and Ekin [10]. It consists essentially in breaking a thin metallic wire by bending the elastic substrate to which it is anchored. The two resulting electrodes are then slowly approached by controlling the strain on the substrate until a contact is recovered. Because this bending set-up is more compact and more rigid than the one of an usual STM, essentially by giving away the possibility of lateral scan, small contacts are significantly more stable with this technique. Furthermore, MCBJs are much easier to implement at low temperature and breaking the wire under cryogenic high vacuum prevents tip or surface contamination.
“Conventional” Mechanical Controllable Break Junctions
The schematic set-up of a MCBJ is depicted in Figure 1. A metallic wire is attached to an elastic substrate (bending beam) of thickness t between two anchors separated by a distance u. The metallic wire presents in between the two anchors a notch. The substrate is placed on two countersupports a distance L apart, and bent by pushing in its center with a pushing rod. The strain imposed on the wire by bending the substrate is geometrically concentrated at the notch. The distance between the two anchors is increased until the metallic wire breaks at the constriction. The two resulting electrodes are then slowly brought back into contact. A simple calculation assuming that the regime is elastic shows that a longitudinal displacementx of the driving rod results in a change in the inter-electrode distance d D r x , where the reduction ratio r 6ut / L2 [11]. Figure 1 “Conventional” mechanically controllable break junction set-up. A notched wire is anchored to an elastic substrate by two droplets of epoxy. It is broken by bending the elastic substrate. For fine adjustment of the distance between electrodes the pushing rod is driven by a piezoelement.
In “conventional” MCBJ, the metallic wire, with a typical diameter between 20 and 200m, is notched with a knife and glued with two droplets of epoxy to the elastic substrate. Typical values are t 1mm and L 20 mm and in practice the distance between the two epoxy anchors cannot be made much smaller than u 0.5 mm , giving rise to a reduction ratio of the order of r 7.103 . After breaking the wire and reestablishing back a contact, the pushing rod is controlled by a piezoelectric actuator to achieve atomic scale control of the interelectrode distance.
The increased stability of the atomic contacts obtained through this technique allowed the team lead by Jan van Ruitenbeek to carry out a wide variety of elegant experiments [4].
Nanofabricated Mechanically Controllable Break Junctions
The technique of nanofabricated MCBJ developed in the Quantronics group at Saclay decreases the reduction ratio even further and thus improves the achievable stability [11]. Using nanofabrication techniques, a metallic film presenting in its center a constriction (see Figure 2) is deposited on an elastic substrate coated with an insulating polyimide layer (see Chapter 2 for the fabrication steps). The polyimide layer is then etched so as to suspend a metallic bridge around the constriction, the large metallic regions remaining anchored to the substrate. Typically the bridge is suspended over 3m and has a 100 nm diameter constriction. For nanofabricated MCBJ, the distance between the two anchors u 3 P is two orders of magnitude smaller than in conventional MCBJ. The much smaller reduction ratio, typically r 9.105 results in an improved stability, allowing to form atomic-size contacts that can be preserved identical for days. This point was essential to the realization of the experiments presented in this thesis because most of measurements required several hours to be completed.
Figure 2: Schematic view of a sample fabricated using electron beam lithography and evaporation techniques. By carving the polyimide layer the bridge is released from the elastic substrate. The large-area metallic regions (anchor pads) remain fixed to the substrate.
Conductance of atomic-size contacts
Conductance steps and plateaus
Figure 3 presents a typical conductance trace obtained while bringing together at constant velocity the two electrodes of an aluminum nanofabricated MCBJ. Measurements were performed at 50 mK under a magnetic field of 200 mT to destroy superconductivity in the aluminum films.
The conductance first increases exponentially (see inset in Figure 3), revealing the tunnel regime in which there is a vacuum gap between the electrodes. This exponential dependence of the conductance allows a precise calibration of the mechanical set-up and a determination of its stability. The measured drift in the interelectrode spacing is of the order of 0.2 pm/h, to be compared to 30 pm/h for conventional MCBJ [11].
At some point the conductance shows a discontinuity that corresponds to a mechanical instability when the two electrodes jump into contact. Afterwards, the conductance evolves through a series of plateaus and sharp steps. The conductance on the first plateau is close to the conductance quantum G0 and the height of the steps is also of the order of G0 . A similar staircase is observed while separating the two electrodes. Although a staircase pattern is observed every time the experiment is performed, the horizontal extension (of the order a fraction of nanometer) and the vertical position of the plateaus are not reproducible for subsequent compression-extension cycles.
To date, these general features have been observed in a large palette of metals [12]: Au, Ag, Cu, Zn, Na, K, Li, Al, Pb, Nb, Sn, …, and under a great variety of experimental conditions (temperature, technique to produce atomic size contacts, rate of compression and extension). The typical conductance on the first plateau, the typical lengths of the plateaus, and the behavior within the plateaus are characteristic of each material. For example, as can be seen in Figure 6 and 3, Al has generally plateaus with negative slope whereas Pb and Nb have mainly positive ones.
Figure 3: Conductance as a function of the relative displacement between the two electrodes while
bringing them closer. Inset: Conductance in the tunnel regime on a logarithmic scale.
The succession of plateaus and conductance jumps is directly related to the dynamics of the atomic configuration of the contact. Combined STM-AFM experiments that measure the force between the tip and the surface simultaneously with the conductance, have beautifully evidenced that on a plateau the atomic configuration is only elastically deformed while a conductance jump results from an abrupt reconfiguration of the atoms at the contact accompanied by a stress relief (see Figure 4). The experimental set-up is depicted in the inset of Figure 4. A clean gold sample is mounted at the end of a cantilever beam. The force between the tip and the gold sample is obtained by measuring the deflection of the cantilever beam with an AFM working in the contact mode. At a conductance step, the contact switches from one atomic configuration to another one. In MCBJ experiments in which the contact is adjusted precisely at a conductance jump, temporal fluctuations between the two atomic configurations, revealed as two levels fluctuations in the conductance, have been observed [13,14].
Molecular dynamics simulations [15,16,17] confirm this interpretation of the staircase pattern. Starting with a perfectly ordered cylindrical metallic wire containing a few thousands atoms, the position of each atom is calculated while the wire is stretched. The atomic structure evolves through a series of stress accumulation phases, in which the relative positions of atoms remain almost constant, and abrupt stress relief phases corresponding to an atomic reconfiguration. During a reconfiguration the lateral dimensions of the contact changes abruptly resulting in a jump of its conductance. Just before breaking, the last and smallest contact corresponding to the last conductance plateau is formed by a single atom (or sometimes a several atom long chain), for which free electron calculations predict a conductance value of the order of G0 [17].
In experiments, the exact conductance of the last plateau is not reproducible from one stretching to another but conductance histograms clearly show a peak at a particular value. In addition, for several metals this peak is very close to G0 . These facts were the first clues that the smallest contacts are indeed one-atom contacts. Other experiments described below have well established this point and provided a deeper insight into electrical transport through a single atom.
Figure 4 (reproduced from [5]): Inset: Schematic representation of the set-up combining an STM and an AFM. Main panel: Representative simultaneous recording of the measured conductance (a) and force (b) during the elongation of an atomic-sized constriction at 300 K. Conductance steps occurs simultaneously with relaxation of the force as a result of atomic rearrangements.
One-atom contacts
Direct observation of one-atom gold contact
In the case of gold, one-atom and chain contacts have indeed been observed directly with Ultra High Vacuum (UHV) high resolution Transmission Electron Microscopes (TEM) [7,8]. Contacts were formed at room temperature using an STM placed at the specimen stage of the UHV TEM. Video images of the atomic structure of the contact have been recorded at high magnification while withdrawing the tip (see Figure 5). They show that the last contact before breaking is constituted from a strand of gold atoms whose conductance is close to G0.
Figure 5 (reproduced from [7]): Electron microscope images of a contact while withdrawing the tip. A gold bridge formed between the gold tip (top) and gold substrate (bottom), thinned from a to e and rupture at f. Dark lines indicated by arrowheads are rows of gold atoms. The faint fringe outside each bridge and remaining in f is a ghost due to interference of the imaging electrons. The conductance of the contact is 0 at f and ~2G0 at e.
This formation of a chain of a few gold atoms was also reported in “standard” STM experiments and MCBJ. By repeating at a high rate many compression-extension cycles, a chain containing up to four or five atoms was sometimes detected, as evidenced by an unusually long last conductance plateau before breaking [18]. The formation of such atomic chains is not completely understood from the molecular dynamics simulation point of view. Furthermore, this phenomenon has been observed only in gold samples and the specificity of this metal compared to others is not well understood.
Direct link between the conductance of a one-atom contact and its chemical valence
As already mentioned the typical conductance value for the smallest contact depends on the material. Conductance histograms, constructed from a large number of conductance traces like the one in Figure 3, show a peak at a particular value, which for monovalent metals like gold, silver, cooper and the alkali metals is close to G0 whereas for lead it is centered at 1.8 G0 and for niobium at 2.3 G0 [12]. The position of this peak is related to the chemical valence of the material.
As described in the following, the number of conduction channels of the last contact can be determined using the highly non-linear current-voltage characteristics in the superconducting state. Experiments performed by three groups have shown that this number of conduction channels is directly related to the number of valence orbital of the metal involved [19]. Four metals, namely lead, aluminum, niobium and gold, were studied covering a large palette of valence structures. In the case of gold, the superconductivity was induced through the proximity effect by a thick aluminum layer in intimate contact with the metallic gold film everywhere but at the constriction [20]. It was found that for gold only one conduction channel contributes to the conductance on the lowest conductance plateau. However, for aluminum and lead, which have p-electrons at the Fermi level, three channels contribute. Niobium is a transition metal with s- and d-electrons, and five conduction channels were found to contribute (see Figure 6).
In order to gain a microscopic insight into the link between conduction channels and the atomic orbital structure, a tight-binding model of a one-atom constriction using an atomic orbital basis was constructed [21,22]. The model includes small random displacements of the atoms around their position in a perfect crystal, but neglects the atom dynamics. Remarkably, despite the fact that the transmission probability of each channel is very sensitive to the exact positions of the atoms in the vicinity of the contact and that the system is not at equilibrium, the number of conduction channels was found to be robust against disorder around the central atom. It is simply determined by its number of valence orbitals. The number of contributing channels predicted by this microscopic calculation is in agreement with experimental results [19].
These theoretical and experimental works firmly established that the smallest possible contact does consist of a single atom, and that the electrical transport properties of one-atom contacts are determined by the chemical nature of the involved atom.
We present now the method used to determine the number of channels. It extracts the complete mesoscopic code of atomic-size contacts from their current-voltage characteristic in the superconducting state.
Full characterization of atomic-size contacts as quantum coherent conductors
As explained in the Appendix B, in the superconducting state the transport through a quantum coherent conductor occurs at small voltages through MAR processes leading to highly non-linear current-voltage characteristics. These non-linearities strongly depend on the transmission of the channels. Since atomic-size contacts accommodate only a small number of channels, their current-voltage characteristic contains enough information to extract their mesoscopic code [23]. We present now the steps leading to the determination of the mesoscopic code and discuss the accuracy of the method.
Determination of the mesoscopic PIN code
The determination is achieved by breaking up the measured current-voltage characteristic I(V) into the contribution of independent channels: I (V ) åiN1 i (V ,i ,) where N is the number of channels, the superconducting gap of the metallic films and i (V , ,) the current-voltage curve calculated for one channel with transmission probability The latter were obtained from the numerical code developed by Cuevas, Martin-Rodero and Levy Yeyati [24]. A least-square fitting procedure is applied with defined as: where D(V) is the density of data points at V in the measured current-voltage characteristic. As the characteristics are non-linear and we do not voltage bias the contact, this density is not at all uniform. One has to take it into account to ensure that the current-voltage characteristic is uniformly weighted. As the size of the voltage interval on which the n-th order MAR process dominates the current is roughly speaking of the order of 2 n e , a uniform density gives more relative weight in to the low order MAR processes. Note however that this imbalance would be worse if the density D(V) were not taken into account. Finally, the maximum voltage of the measured current-voltage characteristics determines the weight attributed to the first order process in the fits. In our fits this voltage is typically of the order of 4 5 / e .
Table des matières
Introduction
Transport through quantum coherent conductors
Atomic contacts as quantum coherent conductors
Josephson supercurrent through a single atom
Shot noise in the current at finite voltage
Dynamical Coulomb blockade
Chapter 1 Metallic atomic-size contacts: fully characterized quantum coherent conductors
1.1 Obtaining atomic-size contacts
1.1.1 The Scanning Tunneling Microscope
1.1.2 The Mechanical Controllable Break Junction technique (MCBJ)
1.1.2.1 “Conventional” Mechanical Controllable Break Junctions
1.1.2.2 Nanofabricated Mechanically Controllable Break Junctions
1.2 Conductance of atomic-size contacts
1.2.1 Conductance steps and plateaus
1.2.2 One-atom contacts
1.2.2.1 Direct observation of one-atom gold contact
1.2.2.2 Direct link between the conductance of a one-atom contact and its chemical valence
1.3 Full characterization of atomic-size contacts as quantum coherent conductors
1.3.1 Determination of the mesoscopic PIN code
1.3.1.1 Measurement of the superconducting gap of the metallic film
1.3.1.2 Fitting procedure to determine the mesoscopic PIN code
1.3.2 Accuracy of the mesoscopic PIN code determination
1.3.3 Uncertainties propagation
1.4 Conclusion
Chapter 2 Experimental techniques
2.1 Nanofabricated break junctions
2.1.1 Wafer preparation
2.1.2 Lithography and metal deposition
2.1.3 Dry etching of the polyimide layer
2.1.4 Embedding a nanofabricated break-junction in an on-chip electromagnetic environment
2.1.4.1 Samples measured in the Josephson supercurrent experiment
2.1.4.2 Sample measured in the Coulomb blockade experiment
2.2 Bending mechanism
2.3 Measurements at low temperature
Chapter 3 Josephson supercurrent through one atom
3.1 The Josephson supercurrent
3.1.1 Current-phase relationship and critical current of various Josephson elements
3.1.2 Current-phase relationship of a quantum coherent conductor
3.1.3 Previous experiments on superconducting atomic-size contacts
3.1.4 Our experiment on Josephson supercurrent in aluminum atomic-size contacts
3.2 Theoretical analysis of the switching process
3.2.1 Qualitative description of the phase dynamics of a DC unshunted atomic-size contact
3.2.2 Solving the phase dynamics
3.2.2.1 Overdamped junction:a0 1
3.2.2.2 Adiabatic regime: a 1
3.2.3 Solving the RSJ model in the overdamped regime
3.2.3.1 Occupation factors of Andreev bound states
3.2.3.2 Ambegaokar-Halperin like calculation
3.2.3.3 Numerical simulation
3.2.3.4 Current-voltage characteristic of a resistively shunted atomic contact
3.2.3.5 Temperature dependence of the supercurrent peak height
3.2.4 Current-voltage characteristics of RC shunted atomic contacts in the overdamped regime
3.3 Measurement of the maximum supercurrent
3.3.1 Measuring switching current histograms
3.3.2 Atomic contacts with not too high transmission probabilities (t < 0.9 )
3.3.3 Atomic contacts with high transmitting channels (t > 0.9 ): the ballistic limit
3.4 Conclusions
Annex: Article published in Physical Review Letters
Chapter 4 Shot noise in atomic-size contacts
4.1 Shot noise in a quantum coherent conductor connecting normal charge reservoirs
4.1.1 Brief review of the theoretical results
4.1.2 Shot noise in quantum point contacts tailored in 2D electron gas
4.1.3 Shot noise in gold atomic-size contacts
4.2 Shot noise in a quantum coherent conductor when superconducting reservoirs are involved
4.2.1 Double electronic charge transfer at a NS interface
4.2.2 SNS junction
4.3 Shot noise measurements in aluminum atomic-size contacts both in the normal and in the superconducting state
4.3.1 Measurement of shot noise in atomic-size contacts
4.3.1.1 Description of the measurement set-up
4.3.1.2 Characterization of the measurement set-up
4.3.1.3 Current fluctuations spectrum deduced from the measured voltage spectrum
4.3.2 Multiple-Charge-Quanta Shot Noise in Superconducting Atomic contacts (reproduced from Phys. Rev. Lett. 86, 4104 (2001))
4.3.3 Complementary analysis
4.3.3.1 Normal state
4.3.3.2 Superconducting state
Annex: Determination of the measurement set-up parameters used in the treatment of the noise spectra
Chapter 5 Dynamical Coulomb blockade
5.1 Coulomb blockade of single electron tunneling
5.1.1 Hamiltonian of a tunnel junction embedded in an electromagnetic environment
5.1.2 Tunneling rates
5.1.3 The distribution function P(e )
5.1.4 Conductance
5.1.5 The RC environment
5.2 Coulomb blockade in a single conduction channel contact
5.3 Measuring dynamical Coulomb blockade in atomic-size contacts
5.3.1 Characteristics of the on-chip electromagnetic environment
5.3.2 Environment impedance
5.4 Experimental results
5.4.1 Mesoscopic code determination
5.4.1.1 Impedance of the superconducting aluminum leads at finite frequency
5.4.1.2 Coulomb blockade of the tunnel superconducting current-voltage characteristic
5.4.1.3 Conclusion
5.4.2 Coulomb blockade in the normal state: the tunnel regime
5.4.3 Coulomb blockade in the normal state: the ballistic regime
5.4.3.1 Coulomb blockade vanishes in the high transmission limit
5.4.3.2 Comparison with the perturbative theory for arbitrary transmission
5.4.3.3 Comparison with the extension of the perturbative result to the non perturbative case
5.5 Conclusion
Appendix A Scattering approach of conductance and shot noise
A.1 The scattering model
A.2 Reduction of the scattering problem to independent conduction channels
A.3 The Landauer formula for the conductance
A.4 Calculation of the shot noise spectral density
A.5 Shot noise: wave packet approach
Appendix B Mesoscopic superconductivity
B.1 The quasiparticles of a BCS superconductor
B.1.1 “Hole description” of the spin down normal quasiparticles
B.1.2 Quasiparticles in the superconducting state
B.2 Andreev reflection
B.3 Andreev bound states: phase biased Josephson junctions
B.3.1 The ballistic Andreev bound states
B.3.2 Andreev bound states in a channel with arbitrary transmission probability t
B.4 Multiple Andreev reflections: voltage biased Josephson junctions