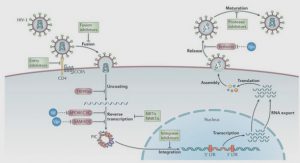
Mesures et incertitudes – Chiffres significatifs
Introduction
La pratique des sciences fondamentales et appliquées conduit à réaliser des mesures.Toute mesure est entachée d’erreurs aléatoires dues au matériel, aux paramètres physiques mis en jeu, et à l’opérateur ; ces erreurs ont des valeurs inconnues et l’on peut seulement les estimer. Les résultats de mesures peuvent être utilisés pour calculer une nouvelle grandeur : le résultat devra être présenté avec un nombre de chiffres significatifs cohérent avec la précision des données.La bonne estimation des erreurs doit conduire à exprimer le résultat de la mesure x d’une grandeur X sous la forme x = ± |Dx| , écrit sous la forme allégée : x = ± Dx , avec Dx > 0.
Dx représente l’incertitude sur la valeur de x,avec un niveau de confiance qui doit être précisé : sa valeur par défaut est 95% .
Exemple 1 : L = 8,2 ± 0,1 cm DL = 0,1 cm :
– la vraie valeur de L a 95% de chances de se trouver dans l’intervalle [8,1 ; 8,3]
– une mesure de L par la même méthode a 95% de chances d’être dans l’intervalle [8,0 ; 8,3]
Exemple 2 : L = 8,20 ± 0,01 cm DL = 0,01 cm :
– la vraie valeur de L a 95% de chances de se trouver dans l’intervalle [ ]
On peut comparer la précision de chacune des mesures données en exemple en calculant une incertitude relative :
Exemple 1 : , soit 1,2 %
Exemple 2 : …………………… soit …………% ; cette mesure est la ………….précise.
On remarque que le zéro après la virgule dans (8,20) a ici de l’importance, il renseigne sur la précision de la mesure, c’est un chiffre significatif.8,2 cm = 0,082 m = 8,2.10… m = ….. mm comporte 2 chiffres significatifs.8,20 cm = 0,0820 m = 8,…..10… m = …….. mm comporte 3 chiffres significatifs.
Exemple 3 : valeur de la constante de gravitation disponible sur le site internet du NIST ( National Institute of standards and Technology)
Newtonian constant of gravitation : G = 6.674 28 x 10-11 m3 kg-1 s-2
Standard uncertainty 0.000 67 x 10-11 m3 kg-1 s-2 : c’est un écart-type associé à 68% de confiance.Relative standard uncertainty 1.0 x 10-4 : c’est-à-dire ……………………………………….Concise form : 6.674 28(67) x 10-11 m3 kg-1 s-2.On écrira aussi : G = …………………… ± ………………. avec un niveau de confiance 68 %
Incertitudes de mesures
Le vocabulaire et les notions employées ici suivent les préconisations du BIMP (Bureau International des Poids et Mesures) précisées dans des documents suivants :
VIM (Vocabulaire International de Métrologie)
GUM (Guide to the expression of Uncertainty in Measurement).Pour une éventuelle spécialisation en métrologie il faut étudier de manière approfondie ces deux documents et un cours de spécialiste en statistiques.
Notions générales
On appelle erreurs de mesure les écarts des résultats par rapport à la valeur vraie.
Ces écarts sont cependant inconnus et ont un caractère aléatoire : on parle d’incertitude.
Cela se manifeste par la dispersion des résultats lorsqu’on répète un grand nombre de fois la mesure d’une même grandeur.
Exemple :
La mesure d’une même intensité a été réalisée avec 22 multimètres identiques.
Les résultats figurent dans le tableau suivant :
I (mA)
| 119,5 | 118,6 | 119,9 | 119,5 | 119,2 | 120,3 | 119,9 | 119,2 | 119,2 | 119,4 | 119,9 |
| 120,0 | 119,0 | 120,1 | 119,8 | 119,4 | 120,5 | 120,1 | 119,4 | 119,4 | 119,5 | 120,1 |
La répartition des mesures est représentée sur l’histogramme ci-dessous : diagramme bâton représentant l’effectif correspondant aux différentes valeurs mesurées. La courbe de Gauss est décrite plus loin.
effectif total n = 22
moyenne = 119,5 mA
min : Imin = 118,5 mA
max : Imax = 120,5 mA
écart-type : s = sn-1 = 0,620 mA
Utiliser les fonctionnalités de la calculatrice pour obtenir l’ensemble des valeurs demandées à droite du tableau. (liste des valeurs dans un tableau, puis calculs de statistique à 1 variable).
Calculs complémentaires :
| nombre | pourcentage | |
| mesures comprises dans l’intervalle [- s ; + s ]
|
||
| mesures comprises dans l’intervalle [- 2s ; + 2s ]
|
||
| mesures comprises dans l’intervalle [- 3s ; + 3s ] |
De nombreuses situations expérimentales montrent que pour un très grand nombre de mesures l’histogramme se rapproche d’une courbe de Gauss, associée à une loi de probabilité nommée « loi normale ».