Etude du resserrement du trou étermination des chargements thermiques induits par le phénomène
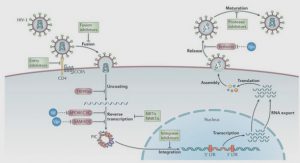
Comme illustré par la Figure IV.1 et expliqué dans la partie introductive concernant l’étude du resserrement du trou en perçage de Ti6Al4V, l’objectif fixé était de déterminer les chargements thermomécaniques issus de l’action des listels sur la paroi du trou. La détermination des chargements mécaniques ayant d’ores et déjà été traitée au chapitre précédent, seuls les chargements thermiques doivent encore être déterminés, à sec et avec assistance cryogénique. Pour cela, il a été décidé d’utiliser une approche hybride, mêlant essais expérimentaux et simulation, afin d’atteindre l’objectif fixé. L’idée était de réaliser, dans un premier temps, des essais de perçage instrumentés en température pour en suivre l’évolution pendant l’opération, puis dans un second temps, d’utiliser un modèle éléments finis (ABAQUS) simulant l’action des listels sur la paroi du trou pour reproduire ces variations de température. L’objectif était de restituer le comportement thermique constaté expérimentalement en faisant varier les données d’entrée du modèle, ici le flux de chaleur entrant dans la pièce qui est la donnée que l’on cherche à déterminer. C’est le principe de la méthode inverse choisie, explicitée par la Figure IV.2 et pour laquelle trois mesures de températures seront réalisées expérimentalement : en entrée, milieu et sortie de trou, à 1 mm de la surface. Ainsi, ce chapitre a pour vocation de détailler les étapes qui ont mené à la détermination des chargements thermiques dans le cadre de l’étude du resserrement du trou en perçage de Ti6Al4V, allant de la conception des campagnes expérimentales, au développement du modèle numérique thermique, jusqu’à la mise en place effective de la méthode inverse pour déterminer les flux thermiques entrants.
Modèles numériques : propriétés, hypothèses et développement
Cette partie a pour vocation de donner des détails concernant les propriétés thermomécaniques et lois de comportement utilisées dans les modèles éléments finis présentés par la suite. De plus, les hypothèses et outils ayant permis la mise en place effective des chargements thermomécaniques dans les calculs éléments finis réalisés seront détaillés. Finalement, des éléments de fonctionnement de la méthode inverse codée sur MATLAB pour la détermination des chargements thermiques seront donnés. Afin de reproduire au mieux le comportement du Ti6Al4V traité β de l’étude, les propriétés mécaniques et thermiques utilisées dans le modèle éléments finis doivent idéalement être thermodépendantes. Par conséquent, l’état de l’art a été sondé dans l’objectif de trouver des valeurs adaptées au matériau de l’étude. En ce qui concerne les données nécessaires à une analyse thermique, [Mills, 2002] propose des valeurs de la densité ρ, de la capacité thermique massique Cp, de la conductivité thermique λ et de la diffusivité D pour le Ti6Al4V de manière générale et ce pour des températures comprises entre 25 et 1000°C. [Ramirez, 2017] quant à lui, a récemment déterminé la capacité thermique massique Cp et la diffusivité D pour le Ti6Al4V traité β correspondant au matériau de l’étude. Ainsi, la Figure IV.3 fait la comparaison de ces propriétés pour les deux auteurs cités précédemment et permet de constater qu’en dessous de 700 °C la différence entre les valeurs qu’ils ont obtenues reste négligeable.
Finalement, il a été décidé d’utiliser les valeurs déterminées par [Mills, 2002] dans les modèles éléments finis développés, sachant que les valeurs de la densité ρ et de la conductivité λ n’étaient pas disponibles dans les travaux de [Ramirez, 2017]. En ce qui concerne l’aspect mécanique, ce sont les valeurs du module d’Young pour des températures comprises entre 25 et 1000 °C que [Ramirez, 2017] a déterminé pour le Ti6Al4V traité β qui seront utilisées. Ainsi, le Tableau IV.1 fait le récapitulatif des valeurs thermodépendantes utilisées dans les modèles éléments finis qui seront présentés. Il est à noter que par manque de données sur le sujet, les propriétés utilisées restent constantes lorsque la température est en-dessous de 25 °C. En outre, le tableau fait figurer les valeurs qui ont été prises constantes pour le coefficient de dilatation thermique et le coefficient de Poisson.