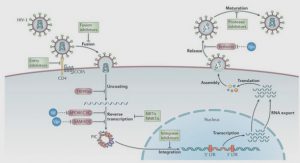
Comportement hydromécanique des joints et du milieu poreux
Un joint dans son ensemble, est considéré comme un volume de l’espace limité par deux surfaces de contact ou épontes. Chaque éponte est localement très irrégulière à cause des variations des formes et l’agencement des grains qui la compose. La position relative des épontes des joints contrôle leur imbrication, et par suite la continuité ou l’absence de zone de contact. En cas d’interruption de la continuité, l’espace vide entre la fracture peut rester vide ou rempli par un matériau. Dans le cas où le vide est rempli, le comportement global de la fracture est lié aux propriétés du matériau de remplissage [Barton et Choubey, 1977]. A l’opposé dans le cas de fracture en contact (non remplie), c’est la rugosité et la résistance en compression des épontes qui contrôlent le comportement global de la fracture. Le comportement mécanique du joint est caractérisé par son comportement sous chargement normale et son comportement en cisaillement. Dans cette partie, on présente les modèles utilisés dans la littérature pour étudier le comportement mécanique sous sollicitation normale des fractures dites remplies ou col- matées et les fractures vides ou ouvertes.De nombreux auteurs ont étudié le comportement des joints sous chargement normal [Shehata et al., 1972; Goodman, 1976; Detournay, 1979; Bandis et al., 1983]. Pour aboutir à des modèles théoriques, ces travaux se sont basés sur des relations qui reproduisent les résultats expérimentaux. Ces essais consistent à évaluer l’évolution du déplacement relatif de la fracture sous un chargement croissant de compression. La plage d’évolution de la contrainte de compression est choisie pour permettre aux roches de rester dans leur phase de déformation élastique pendant les essais. Sous-chargement normal cyclique, Goodman [1976], et Bandis et al. [1983] montrent que le comportement du joint est fortement non- linéaire avec une forme hyperbolique (voir figure 2.1). Bandis et al. [1983] ont montré que les joints ouverts sont plus déformables que les joints colmatés (voir figure 2.1(b)) avec également un comportement non-linéaire. L’aug- mentation de la contrainte normale créée de nouvelles zone en contact par déformation élastique, plastique irréversible et ou écrasement des aspérités [Goodman, 1974; Plesha, 1987]. La relation proposée par Bandis et al. [1983] pour ajuster les résultats des essais aux laboratoires des fractures ouvertes sous chargement normal est de la forme semi- logarithmique :
Modèles de comportement des joints sous chargement de cisaillement
Ces essais avaient pour but d’évaluer l’effet de la rugosité sur le comportement en cisaillement de la fracture. Suivant le niveau de contraintes appliqué, il a formulé deux modèles de rupture différents. Pour de faibles valeurs de contrainte, le mouvement relatif entre les lèvres de la frac- ture est un glissement suivant la direction positive des aspérités. En d’autres termes, les aspérités se glissent l’une sur l’autre et le comportement de la fracture est donné par la pente du segment supérieur (φµ + i) dans la figure 2.2. L’équation de la résistance s’écrit alors : Le modèle formulé par Ladanyi et Archambault [1969] est une extension de celui de Pat- ton. Il combine le frottement, la dilatance et la résistance des aspérités lors du cisaillement du joint dans un modèle contrainte-dilatance. A partir des travaux de Rowe et Barden [1964], Ladanyi et Archambault [1969] postulent que la force tangentielle au pic Sp, est la somme de 4 composantes. La somme des trois premières composantes S1 + S2 + S3 est la répartition du glissement des aspérités sur l’aire A − As et la quatrième composante S4avec, S1 = N v, la composante de cisaillement due au travail externe en dilatance contre la force normale, S2 = Sv tan ϕf , la composante du cisaillement due au travail interne additionnel en frottement due à la dilatance, S3 = N tan ϕb, la composante du cisaillement due au travail interne en frottement si l’échantillon ne change pas de volume au cours du cisaillement et S4 = Aτca, la composante due au cisaillement des aspérités. Dans les composantes du cisaillement le terme N désigne la force normale, v le taux de dilatance à la rupture (dépendant de l’angle de dilatance à la rupture), S la force tangentielle, ϕfl’angle de frottement à la rupture totale des épontes, ϕb l’angle de frottement de base, A la surface totale d’une éponte et τca la résistance au cisaillement des aspérités.