Application à la maquette VeRCoRs

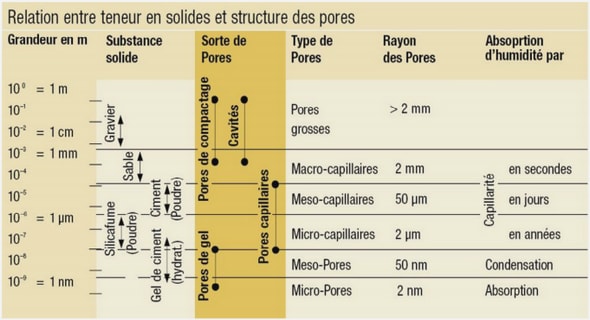
Application à la maquette VeRCoRs

Maillage

 Dans l’optique d’une mise en œuvre industrielle et de temps de calculs raisonnables, le maillage le moins raffiné fourni dans le cadre du benchmark VeRCoRs est linéarisé avant d’être utilisé pour la modélisation de l’ensemble des phénomènes thermo-hydro-mécaniques, ainsi que pour le calcul du débit de fuite. (a) Câbles de précontrainte (b) Béton de l’enceinte interne (c) Zoom dans l’épaisseur Fig. 3.1 : Maillage EF utilisé pour modéliser le comportement de la maquette VeRCoRs 40 cm 68 Application à la maquette VeRCoRs Modélisation et prévision du comportement thermo-hydro-mécanique d’une paroi en béton Application au cas des enceintes de confinement des bâtiments réacteurs nucléaires Ce maillage contient 34694 nœuds dans les EF 3D du béton et 16066 nœuds dans les EF 1D des câbles de précontrainte. Les 295 câbles horizontaux, verticaux, gamma et spécifiques au dôme de la maquette sont pris en compte ainsi que leurs déviations (Fig. 3.1a). Les armatures passives ne sont pas maillées. Les principales zones singulières de béton d’une enceinte interne sont également maillées : traversées et surépaisseur au niveau du TAM, surépaisseurs du gousset, du corbeau du pont polaire et de la ceinture torique, nervures d’ancrage des câbles de précontrainte. Malgré une discrétisation du béton relativement grossière dans les directions horizontales et verticales (Fig. 3.1b), la discrétisation par dix éléments de taille évolutive dans les 40 cm d’épaisseur de la jupe (Fig. 3.1c) est adaptée à la représentation des phénomènes liés au séchage de la structure et permettra de démontrer l’applicabilité de la stratégie par macroéléments. 

Paramètres de la modélisation

 La stratégie proposée visant à calculer le débit de fuite à long terme de la structure, seules les propriétés du béton durci sont prises en compte dans l’ensemble des calculs effectués (pas d’évolution au jeune âge). La durée de vie de la maquette étant relativement courte comparée à une structure réelle, les propriétés matériau utilisées sont supposées constantes dans le temps. Un grand nombre de données et caractérisations a été fourni dans le cadre du benchmark VeRCoRs. Lorsqu’elles sont disponibles, les moyennes des paramètres mesurés par levée lors de la construction sont utilisées dans les calculs. A défaut, les résultats des laboratoires partenaires ou les données fournisseur sont utilisées. 

Calcul thermique 

Tous les paramètres d’entrée du calcul thermique sont récapitulés dans le Tab. 3.1. Paramètre Symbole Valeur Unité Masse volumique 𝜌𝑏 2395 kg∙m-3 Capacité thermique 𝐶𝑝 880 J∙kg-1 ∙K -1 Conductivité thermique 𝜆(𝑇) 6,77 T – 239 10-3 W∙m-1 ∙K -1 Coefficient d’échange convectif ℎ𝑐 8 W∙m-2 ∙K -1 Tab. 3.1 : Caractéristiques thermiques du béton 

 Modélisation et prévision du comportement thermo-hydro-mécanique d’une paroi en béton Application au cas des enceintes de confinement des bâtiments réacteurs nucléaires La valeur de 𝜌𝑏 est la moyenne des masses volumiques mesurées sur chaque levée de l’enceinte. Les valeurs de 𝐶𝑝 et 𝜆 sont directement identifiées en laboratoire. La valeur de ℎ𝑐 est fournie par EDF. 

Calcul hydrique 

Tous les paramètres d’entrée du calcul hydrique sont récapitulés dans le Tab. 3.2. Paramètre Symbole Valeur Unité Viscosité dynamique de l’eau 𝜂𝑙 1,002∙10-3 Pa∙s Porosité du béton 𝜙 0,146 – Energie d’activation 𝐸𝑎 28000 J∙mol-1 Constante des gaz parfaits 𝑅 8,314 J∙mol-1 ∙K -1 Température de référence 𝑇 𝑟𝑒𝑓 20 °C Masse volumique de l’eau liquide 𝜌𝑙 998,3 kg∙m-3 Masse molaire de l’eau 𝑀𝑙 18∙10-3 kg∙mol-1 Perméabilité intrinsèque à l’eau du béton 𝐾𝑖𝑛𝑡 𝑙 6,074∙10-20 m 2 Paramètres du modèle de Van Genuchten 𝑛 1,301 – 𝑃𝑟 17,61 MPa Tab. 3.2 : Paramètres pour la diffusion de l’eau dans le béton Les paramètres 𝜂𝑙 , 𝑅, 𝜌𝑙 et 𝑀𝑙 ont des valeurs de référence. La valeur de 𝐸𝑎 est directement identifiée en laboratoire sur un essai maturométrique et 𝑇 𝑟𝑒𝑓 est la température à laquelle toutes les propriétés matériau sont mesurées. La valeur de 𝜙 est la moyenne des porosités mesurées sur chaque levée de l’enceinte. En général, une isotherme de désorption du béton permet d’identifier les paramètres 𝑛 et 𝑃𝑟 indépendamment de 𝐾𝑖𝑛𝑡 𝑙 , identifié ensuite sur une courbe de perte en masse. La courbe isotherme fournie par le benchmark n’étant que partielle (3 points de mesure au-dessus de 85 % d’humidité relative) et caractérisée à 60 °C, son interpolation aux conditions de pression et température représentatives d’une EI est rendue très difficile [36]. Les trois paramètres ont alors été identifiés simultanément sur un essai de suivi de la masse d’une éprouvette cylindrique d’1 m de long et 70 Application à la maquette VeRCoRs Modélisation et prévision du comportement thermo-hydro-mécanique d’une paroi en béton Application au cas des enceintes de confinement des bâtiments réacteurs nucléaires 16 cm de diamètre placée à 20 °C et 50 % d’HR. L’essai est modélisé par EF avec l’équation (2.3) dont les paramètres inconnus sont recalés par une méthode de descente (Levenberg-Maquardt [6]) qui minimise une fonctionnelle de l’écart entre courbes expérimentale et numérique (au sens des moindres carrés). L’identification numérique est comparée aux mesures expérimentales en Fig. 3.2. Fig. 3.2 : Calage des paramètres 𝐾𝑖𝑛𝑡 𝑙 , 𝑛 et 𝑃𝑟 sur un essai de perte en masse La cinétique de perte en eau du béton identifiée en Fig. 3.2 semble appropriée. Toutefois, l’algorithme utilisé montre que l’influence du paramètre 𝑛 sur le calage est prépondérante devant celle de 𝑃𝑟 puis de 𝐾𝑖𝑛𝑡 𝑙 . En effet, plusieurs jeux de paramètres (𝑛, 𝑃𝑟 ,𝐾𝑖𝑛𝑡 𝑙 ) peuvent permettre d’identifier la même courbe de perte en masse mais aboutir à des cinétiques de dessiccation différentes [97], justifiant le besoin d’une identification en deux étapes dès que des données expérimentales complémentaires seront disponibles.

Calcul mécanique

Câbles de précontrainte 

Tous les paramètres utilisés pour caractériser les câbles de précontrainte sont fournis par leur fabricant et récapitulés dans le Tab. 3.3. 46,1 46,3 46,5 46,7 46,9 47,1 47,3 0 30 60 90 120 150 180 210 240 Masse (kg) Temps (j) Expérimental Modèle Modélisation et prévision du comportement thermo-hydro-mécanique d’une paroi en béton Application au cas des enceintes de confinement des bâtiments réacteurs nucléaires Paramètre Symbole Valeur Unité Module d’Young 𝐸𝑠 190 GPa Section (4T15) 𝐴𝑠 556 mm2 Masse volumique – 7800 kg∙m-3 Résistance à rupture 𝑓𝑝𝑘 1860 MPa Tension initiale 𝐹0 848 (1525) kN (MPa) Coefficient de relaxation à 1000 h 𝜌1000 2,5 % Coefficients de frottement 𝜇 0,16 (verticaux, gamma et dôme) 0,17 (horizontaux) – Coefficients de pertes linéiques 𝑘 5 (verticaux) 9,38 (gamma et dôme) 8,82 (horizontaux) 10-3 m -1 Recul d’ancrage – 8 mm Tab. 3.3 : Caractéristiques mécaniques des câbles de précontrainte 

Béton 

L’ensemble des paramètres utilisés pour le comportement du béton est récapitulé dans le Tab. 3.4.

 Données fournies dans le cadre du benchmark 

Les valeurs de 𝐸, 𝛼𝑡ℎ et 𝑓𝑡 sont les moyennes des propriétés mesurées pour chaque levée de l’enceinte. La masse volumique du béton armé 𝜌𝑏𝑎 est la moyenne des mesures de chaque levée 𝜌𝑏 (Tab. 3.1) à laquelle on ajoute forfaitairement 100 kg∙m-3 pour prendre en compte l’influence des armatures passives, non maillées dans le modèle proposé. La valeur de 𝐸𝑎 𝑙 est celle proposée par Hilaire [53]. La valeur de 𝐺𝑓 est directement identifiée en laboratoire. Sans information expérimentale disponible permettant leur identification, les valeurs de 𝜈, 𝜈𝑓𝑝, 𝛼𝑓𝑝, 𝐴𝑡 , 𝐴𝑐 , 𝐵𝑐 et 𝜒 sont proposées par défaut. 𝐵𝑡 est définie pour chaque maille selon la procédure décrite en section 2.4.2.6. Avec les valeurs choisies, l’effet Poisson spécifique au fluage propre, la dissymétrie entre fluage en traction et en compression et le fluage tertiaire (couplage entre 72 Application à la maquette VeRCoRs Modélisation et prévision du comportement thermo-hydro-mécanique d’une paroi en béton Application au cas des enceintes de confinement des bâtiments réacteurs nucléaires endommagement et fluage total du béton) ne sont pas pris en compte dans le calcul réalisé. Paramètre Symbole Valeur Unité Module d’Young 𝐸 36,85 GPa Coefficient de Poisson élastique 𝜈 0,2 – Masse volumique 𝜌𝑏𝑎 2495 kg∙m-3 Coefficient de retrait de dessiccation 𝜅𝑟𝑑 1,027∙10-3 – Coefficient de dilatation thermique 𝛼𝑡ℎ 12,2∙10-6 K -1 Coefficient de Poisson de fluage propre 𝜈𝑓𝑝 0,2 – Amplification du fluage propre en traction 𝛼𝑓𝑝 1 – Chaîne de Burger pour le fluage propre 𝑘𝑟𝑒𝑣 168,2 GPa 𝜂𝑟𝑒𝑣 141,8∙106 GPa∙s 𝑘𝑖𝑟𝑟 81,63 GPa Coefficient de fluage de dessiccation 𝜅𝑓𝑑 6,897∙10-11 Pa-1 Energie d’activation du fluage à court terme 𝐸𝑎 𝑙 18700 J∙mol-1 Energie de fissuration 𝐺𝑓 100 N∙m-1 Limite élastique en traction 𝑓𝑡 3,89 MPa Endommagement en traction 𝐴𝑡 0,9 – Endommagement en compression 𝐴𝑐 1,25 – 𝐵𝑐 600 – Couplage fluage-endommagement 𝜒 0 – Tab. 3.4 : Caractéristiques mécaniques du béton Le suivi des déformations en laboratoire de trois éprouvettes cylindriques (1 m de long, 16 cm de diamètre), fourni dans le cadre du benchmark, permet d’identifier de manière progressive le comportement différé du béton VeRCoRs. Modélisation et prévision du comportement thermo-hydro-mécanique d’une paroi en béton Application au cas des enceintes de confinement des bâtiments réacteurs nucléaires

 Identification du modèle de retrait de dessiccation 

Tout d’abord, un essai de retrait de dessiccation à 50 % d’humidité relative après 90 jours de scellement est modélisé par EF avec l’équation (2.14) pour caler le coefficient 𝜅𝑟𝑑 (Fig. 3.3). Fig. 3.3 : Calage du paramètre 𝜅𝑟𝑑 sur un essai de retrait de dessiccation La Fig. 3.3 montre que le modèle choisi pour représenter le retrait de dessiccation, malgré son utilisation classique dans la littérature, n’est pas parfaitement adapté à la formulation VeRCoRs au cours des premiers mois de séchage. En effet, l’unique paramètre de ce modèle ne permet pas de caler simultanément la déformation à long terme et la cinétique de retrait mesurées. Un choix intermédiaire (qui pourra être revu avec des données supplémentaires) a été réalisé en Fig. 3.3. Toutefois, dans le cadre de la stratégie globale proposée, qui vise des applications jusque 40 ans et au-delà, la cinétique initiale du retrait n’aurait que peu d’impact sur la déformation maximale atteinte et le modèle utilisé reste acceptable en première approche. 

Identification du modèle de fluage propre

 Dans une deuxième étape, un essai de fluage sous 12 MPa de compression appliqués à partir de 90 jours en conditions endogènes permet de caler les coefficients 𝑘𝑟𝑒𝑣, 𝜂𝑟𝑒𝑣 et 𝑘𝑖𝑟𝑟 des équations (2.19) à (2.21). Dans l’absolu, les composantes réversible et irréversible devraient être identifiées de manière -500 -450 -400 -350 -300 -250 -200 -150 -100 -50 0 90 120 150 180 210 240 270 300 330 360 390 Déformation (x10 -6 ) Temps (j) Expérimental Modèle 74 Application à la maquette VeRCoRs Modélisation et prévision du comportement thermo-hydro-mécanique d’une paroi en béton Application au cas des enceintes de confinement des bâtiments réacteurs nucléaires indépendante grâce à une décharge au cours de l’essai de fluage [53]. Cette information n’étant pas disponible dans le cadre du benchmark, les trois paramètres ont été identifiés simultanément (Fig. 3.4). Fig. 3.4 : Calage des paramètres 𝑘𝑟𝑒𝑣, 𝜂𝑟𝑒𝑣 et 𝑘𝑖𝑟𝑟 sur un essai de fluage sans séchage D’après la Fig. 3.4, la chaîne rhéologique utilisée pour le modèle de fluage propre permet de bien reproduire les déformations mesurées expérimentalement. 

Identification du modèle de fluage de dessiccation 

Connaissant désormais de manière indépendante le comportement en dessiccation et en fluage propre du béton VeRCoRs, il reste à identifier la composante de fluage de dessiccation permettant de retrouver les déformations totales au cours d’un essai de fluage sous 12 MPa et 50 % d’humidité relative imposés à partir de 90 jours. L’essai est modélisé par EF avec l’ensemble des identifications précédentes et l’équation (2.22) pour caler le paramètre 𝜅𝑓𝑑 (Fig. 3.5). Du fait du choix d’une modélisation indépendante des phénomènes pour la prédiction des déformations du béton, l’impact du modèle de retrait de dessiccation reste sensible sur les déformations totales de la Fig. 3.5. Le modèle de fluage de dessiccation utilisé ne comportant qu’un seul paramètre, il n’est pas possible de lui trouver une valeur permettant de caler parfaitement la -700 -600 -500 -400 -300 -200 -100 0 90 120 150 180 210 240 270 300 330 360 390 Déformation (x10 -6 ) Temps (j) 

Expérimental Modèle

 Modélisation et prévision du comportement thermo-hydro-mécanique d’une paroi en béton Application au cas des enceintes de confinement des bâtiments réacteurs nucléaires cinétique de retrait tout en estimant correctement le niveau de déformation à long terme.