Champ des ondes de surface à l’aide du formalisme de Green

Champ des ondes de surface à l’aide du
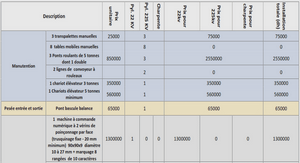
formalisme de Green

Introduction originale

Surface plasmons have been known since the pioneering work of Ritchie in the 1950s (R 1957). Considerable advances made in nanotechnology in recent years and the desire to control and manipulate light at nanoscale have renewed the interest in surface plasmons (B et al. 2003). Numerical simulations and experiments have demonstrated unique properties of different plasmonic nanostructure such as extraordinary transmission (E et al. 1998 ; L et L 2008), guiding (W et al. 2001 ; B e al. 2006 ; Q et al. 1998 ; M et al. 2003), ìuorescence enhancement (A et B 2001 ; A et al. 2006 ; K et al. 2006 ; R et al. 2005b ; K et al. 2008), ëeld enhancement (T et al. 2005 ; P et al. 2003 ; K et al. 2003), focussing (L et al. 2005), superresolution (F et al. 2005 ; S et al. 2005 ; T et al. 2006b), omnidirectional absorption (T et al. 2008 ; M et al. 2004), coherent thermal emission (G et al. 2002 ; M et al. 2004 ; L et al. 2005). In this paper, we shall focus on surface plasmons propagating along ìat surfaces. Propagation of surface plasmons on a ìat surface perpendicular to the z axis is often discussed using a mode E(z)exp[i(Kxx+Kyy− ωt)] characterized by a frequency ω and a wave vector K = Kx^x + Ky^y parallel to the interface. However, the surface plasmon ëelds diffracted by edges, guided by ridges, focussed by lenses cannot be described by a simple mode. It is well-known that a ënite size beam propagating in a vacuum has to be described in terms of a linear superposition of plane waves. Differents ansatz, often neglecting polarization, have been used in the litterature to address this question (W et al. 2001 ; F et al. 2007 ; Z et B 2007). One of the goals of this paper is to derive a rigorous representation for the surface plasmon ëeld. Such a superposition is the equivivalent of the angular plane wave spectrum for surface plasmons It can be used to develop a framework for surface plasmon Fourier optics. In doing so, a difficulty arises. When losses are taken into account, a mode with real K and real ω is no longer a valid solution. Although we can still use a Fourier representation with real K and real ω, it is not convenient to deal with waves that are not a solution. Elementary solutions using either a complex K or a complex ω can be found. However, we cannot assume that they form a basis. e ërst issue is thus to derive a general representation for the surface plasmon ëeld as a superposition of modes. e second issue is related to the dispersion relation. A dispersion relation can be found when using either a complex K and a real ω or vice versa. ese two choices leads to different shapes as seen in Fig.1.2. One dispersion relation has an asymptote for very large values of K while the other has limited values of K and presents a backbending. is issue was ërst noted by Arakawa et al. (A et al. 1973) and later discussed by Alexander et al. (A et al. 1974). Alexander remarked that when plotting the position of the dips in a reìectivity experiment where the angle of incidence is varied at ëxed frequency, one ënds the dispersion relation with backbending. Instead, when plotting the points obtained from a spectrum at ëxed angle, one ënds the dispersion relation without backbending. is approach seems simple and easily applicable. It is sufficient to explain the attenuated total reìection (ATR) experiments. Nevertheless, it is not a general prescription that can be used to discuss all possible issues. Let us illustrate this point by addressing two questions regarding the most important properties of surface plasmons : conënment of the ëelds and large density of states. For a theoretical discussion of these applications, different dispersion relations lead to different predictions. Conënment of the ëeld is the key property regarding applications such as optical lithography, enhanced non-linear effects or super-resolution issues. e dispersion relation with a backbending predicts a cut-off spatial frequency and therefore a resolution limit whereas the dispersion relation without backbending does not predict any resolution limit. Enhancement of the local density of states (or Purcell effect) is fundamental for ìuorescence enhancement and more light emission assisted by surface plasmons. e dispersion relation with a backben- ding again predicts a cut-off spatial frequency and therefore an upper limit to the LDOS. No limit is predicted by the other dispersion relation. A general discussion on the applicability of the different dispersion relations is thus needed. In this paper we start by deriving two general representations of the surface plasmon ëeld in terms of linear superpositions of modes having the structure exp[i(Kxx+Kyy+γz−ωt)] with a well-deëned polarization. Each representation is associated with either a complex frequency or a complex wavevector and therefore to a particular dispersion relation. We then show that the most convenient choice depends on the physical problem to be discussed. We introduce a prescription that allows to choose complex or real frequency and the associated dispersion relation. We then apply our analysis to discuss the resolution limit issue and the LDOS issue. e paper is organized as follows. For the sake of completeness, we brieìy summarize the derivation of the dispersion relation in the next section. e following section introduces the general representations of the surface plasmon ëeld. We then discuss the physical content of these representations. 

Surface plasmon dispersion relation

Let us consider a ìat metal surface z = 0 bounded by dielectric media with dielectric constant ε1. For convenience, we describe the dielectric response of the metal to an electric ëeld using the local Drude model where ωp is the bulk plasmon frequency and νe is a phenomenological bulk electron relaxation rate. We derive the dispersion relation of surface plasmons propagating along the metal/dielectric interface. We search a solution of Maxwell equations for an interface between two linear isotropic and local media characterized by dielectric constants ϵm where m = 1, 2 denotes medium 1 (z < 0) or 2 (z > 0). A surface wave solution has a structure exp[i(K · r + γm|z| − ωt)] with K 2 + γ 2 m = ϵmω 2 /c 2 (1.2) where γm is chosen so that Imγm > 0. Boundary conditions impose the continuity of the tangential components of the electric ëeld and ϵEz. It follows that a p-polarized ëeld can exist provided that ϵ1γ2 = −ϵ2γ1. One ënds that a solution is given by K2 = (ω c )2 ϵ1ϵ2 ϵ1 + ϵ2 . (1.3) When dealing with an interface separating a dielectric from a non lossy metal, ϵ1ϵ2 ϵ1 + ϵ2 yields a unique solution to the problem. When accounting for losses in the material, ϵ1ϵ2 ϵ1 + ϵ2 is a complex number so that the dispersion relation cannot be solved using real K and real ω. It is necessary to consider a complex frequency or a complex wavector to ënd roots of the equation. Let us ërst choose ω real. We denote Ksp the complex root of the equation (4.4). Fig.1.2(a) shows the dispersion curve obtained from the surface plasmon dispersion relation Eq. (4.4) when plotting ω versus ReKsp. is curve exhibits a back-bending in the vicinity of the frequency of non-retarded surface plasmon ωp/ √ 2. e second possible choice is to keep a real wavector K. We denote ωsp the complex root of the equation Eq. (4.4). Fig.1.2(b) shows the dispersion curve obtained when plotting Reωsp versus K. It is seen in Fig.1.2(b) that this curve exhibits an asymptote for large wavevectors. Let us make two remarks regarding the dispersion relation. We ërst note that Eq.(4.4) is also a solution of ϵ1γ2 = ϵ2γ1 which deënes a zero of the reìection factor, i.e. the Brewster angle. It can be checked that the upper branch in Fig.1.2(b) is not a surface wave but the locus of the Brewster angle in the (ω, K) plane. Finally, we note that a surface plasmon is a collective oscillation of charge density. When the frequency ω is smaller than νe, the collective electron oscillation is overdamped. In this frequency regime, Eq.(4.4) describes a surface wave that has no longer the character of a surface plasmon. us, Eq.(4.4) describes the Brewster angle for ω > ωp, a surface plasmon for ωp > ω > νe, a surface wave for νe > ω. 

 General íeld representations e aim of this section is to derive a general form of the surface plasmon ëeld. To this aim, we ërst use the simple interface Green’s tensor that yields the general form of the ëeld for any given source distribution. We then extract the surface plasmon contribution which is deëned to be the pole contribution to the Green’s tensor. We will show that this procedure leads in a natural way to different representations that make use of either a complex wavevector or a complex frequency. We emphasize that both representations will describe the same electromagnetic surface plasmon ëeld Esp(x, y, z, t). 

Let us suppose that an arbitrary source is located nearby the dielectric-metal interface. e electric ëeld generated by the source j(r, t) is given by the relation E(r, t) = −µ0 ∫ dt ′ ∫ d 3 r ′ ←→G (r,r ′ , t − t ′ ) ∂j(r ′ , t′ ) ∂t′ , (1.4) where µ0 is vacuum permeability. A Fourier representation can be written in the form ←→G (r,r ′ , t − t ′ ) = ∫ d 2K 4π 2 ∫ dω 2π ←→g (K, z, z′ , ω)e i[K(r−r ′ )−ω(t−t ′ )] , (1.5) Here, the integration variables ω and Kx, Ky are real. e explicit form of the Green’s tensor ←→g (K, z, z′ , ω) in the presence of the interface is given in Appendix A. It is seen that the Fourier transform of the Green’s tensor has poles given by the denominator of the Fresnel factors for p-polarized ëeld. For a dielectric/metal interface, they correspond to the surface plasmon as discussed previously. us, the Green’s tensor can be split into two terms : the pole contribution that yields the surface plasmon and the remaining contribution that yields a regularized Green’s tensor. ←→G = ←→G reg + ←→G sp, (1.6) where the pole contribution to the Green’s tensor ←→G sp can be explicitly derived using the residue theorem. ←→G reg is the contribution of the regularized Green’s dyadic. It can be shown that the Green’s tensor can be evaluated using a contour deformation in the complex plane and that the regularized term is essentially due to the contribution along the branch cut. is contribution is often termed cylindrical wave or creeping wave. e relative importance of these terms is well documented in classical texts for radiowaves (B 1966 ; F et M 1994). e analysis of their respective contribution was of practical importance in the early days of telecommunications as radiowaves were guided by the earth. is issue has been discussed recently in the context of optics (L et H 2006 ; L et L 2008). In this paper, we shall not pursue this discussion and focus instead on the surface wave contribution deëned as the pole contribution. Esp(r, t) = −µ0 ∫ dt ′ ∫ d 3 r ′ ←→G sp(r,r ′ , t − t ′ ) ∂j(r ′ , t′ ) ∂t′ . (1.7) When solving Eq.(4.4), we can consider that ω is real and ënd a complex Ksp or we can impose a real value to K and ënd a complex root ωsp. us, when extracting the poles, it is a matter of choice to consider that they are poles in the complex frequency plane or in the complex wavevector plane. We ënd either a couple of poles ωsp and −ω ∗ sp or a complex wavevector pole K2 sp hence two poles for the component of the wavevector along the x axis Kx,sp and −Kx,sp for a given component along the y axis Ky as K2 sp = K2 x,sp+K2 y . It follows that we can cast the pole contribution to the Green’s tensor in the form : ←→g sp(K, z, z′ , ω) = ←→f ωsp (K, z, z′ ) ω − ωsp + ←→f −ω∗ sp (K, z, z′ ) ω + ω∗ sp , (1.8) 

General íeld representations

 where ←→f ωsp (K, z, z′ ) and ←→f −ω∗ sp (K, z, z′ ) are the residues of ←→g at ωsp and −ω ∗ sp respectively, or in the form : ←→g sp(K, z, z′ , ω) = ←→f Kx, sp (Ky, z, z′ , ω) Kx − Kx, sp + ←→f −Kx, sp (Ky, z, z′ , ω) Kx + Kx, sp where ←→f Kx, sp (Ky, z, z′ , ω) and ←→f −Kx, sp (Ky, z, z′ , ω) are the residues of ←→g at Kx, sp and −Kx, sp respectively. ese two choices leads to two different forms of the surface plasmon ëeld given by Eq.(1.7). We now examine these forms in detail.

Surface plasmon íeld representation with a real wavevector

 In this section we derive the analytical form of the surface plasmon ëeld using real wavevectors. For this purpose we evaluate the pole contribution to the Green’s tensor by integrating in the complex ω plane. e complex pole ωsp then yields a contribution for t−t ′ > 0 that varies as exp(−iωsp(t−t ′ )). After integration, we ënd : ←→G sp = H(t − t ′ ) 2Re ∫ d 2K (2π) 2 (−i) ←→f ωsp (K, z, z′ )e i[K·(r−r ′ )−ωsp(t−t ′ )] (1.9) where ←→f ωsp (K, z, z′ ) is the residue of ←→g at ωsp. It is given in the appendix C.1. It follows from Eq.(1.7) that the ëeld can be cast in the form of a linear superposition of modes with real wavevector and complex frequency : Esp = 2Re ∫ d 2K (2π) 2 E(K, t)(Kˆ − K γm nm)e i(K·r+γm|z|−ωspt) , (1.10) where the amplitude E(K, t) is given in appendix C.1, nm = −^z if z < 0 and ^z if z > 0, and K^ = K/K. e surface plasmon ëeld takes a form that looks as a mode superposition except that the amplitude E(K, t) depends on the time t. Indeed, when describing a stationary ëeld using modes that have an exponential decay, the amplitude is necessarily time dependent. In order to obtain a superposition of modes with ëxed amplitudes, it is necessary to assume that all sources are extinguished after time t = 0 so that we observe the ëeld after it has been excited. In that case, the decay of the mode is well described by the imaginary part of ωsp. Eq. (1.10) is thus well suited for ëelds excited by pulses. Note that the polarization of each mode is speciëed by the complex vector Kˆ − K γm nm, whose component along the z axis depends on the medium from which the ëeld is evaluated.

Surface plasmon íeld representation with a real frequency

 Let us now turn to the alternative choice. We consider the complex poles Kx, sp and −Kx, sp. e Green function can be cast in the form : ←→Gsp = i ∫ dω 2π ∫ dKy 2π ←→f Kx, sp (Ky, z, z′ , ω)e iKx, sp(x−x ′ ) e iKy(y−y ′ ) e −iω(t−t ′ ) (1.11) 12 Chapitre 1. Champ des ondes de surface à l’aide du formalisme de Green [Phys. Rev. B 79, 195414 (2009)] if x − x ′ > 0, and : ←→Gsp = −i ∫ dω 2π ∫ dKy 2π ←→f −Kx, sp (Ky, z, z′ , ω)e −iKx, sp(x−x ′ ) e iKy(y−y ′ ) e −iω(t−t ′ ) (1.12) if x − x ′ < 0. ←→f Kx, sp (Ky, z, z′ , ω) and ←→f K−x, sp (Ky, z, z′ , ω) are the residues of ←→g at Kx, sp and −Kx, sp. ey are given in appendix C.1. When inserting this form in Eq.(1.7), we again obtain a form for the ëeld that is a superposition of modes whose amplitude depends on x : E = ∫ dω 2π ∫ dKy 2π [ E>(Ky, ω, x)(K^+ − Ksp γm nm)e i(Kx, spx+Kyy+γm|z|−ωt) + E<(Ky, ω, x)(K^− − Ksp γm nm)e i(−Kx, spx+Kyy+γm|z|−ωt) ] (1.13) where K^+ = (Kx,sp^x + Ky^y)/Ksp and K^− = (−Kx,sp^x + Ky^y)/Ksp. e amplitudes E>(Ky, ω, x) and E<(Ky, ω, x) are given in appendix C.1. Again, it seems natural to have amplitudes of the modes that depend on x if one describes a homogeneous ëeld using modes with a decay along x. A proper mode representation should use only ëxed amplitudes. is is possible if all the sources lie in the x < 0 region and the region of interest is the x > 0 region. We then obtain a surface plasmon ëeld that can be cast in the form : E = ∫ dω 2π ∫ dKy 2π (K^ − Ksp γm nm)E>(Ky, ω)e i(K·r+γm|z|−ωt) (1.14) where K = Kx, sp^x + Ky^y is complex and K^ = K/Ksp. We conclude that stationary monochromatic ëelds with a ënite size are well described by a representation that uses complex wavevectors and real frequencies. is equation is one of the main result of this paper. Indeed, it provides a framework to develop surface plasmon Fourier optics. Similar representations have been postulated as ansatz to surface plasmons interferences (Z et B 2007), propagation along a stripe (W et al. 2001) or focussing (F et al. 2007). e framework introduced above provides a rigorous derivation of the form of the surface plasmon ëeld valid in a region with no sources. Let us emphasize that this representation is well suited to discuss propagation for x > x0 of a surface plasmon ëeld known along a line x = x0. It is seen on Eq.(1.14) that propagation over a distance d amounts to multiply each mode by a factor exp(iKxd). In general, this involves modifying both the phase and the amplitude of the mode. us, it allows to discuss any surface wave diffraction problem. Finally, let us stress that this representation is valid for a complex wavevector K and a real frequency ω so that this representation is necessarily associated with a dispersion relation with backbending. To summarize, we have shown that the surface plasmon ëeld can be represented using modes that have either a complex frequency or a complex wavevector. However, the amplitudes may still depend on either time or space. In the case of a ëeld excited by a pulse, the representation that uses a complex frequency is well suited. It is associated with the dispersion relation without backbending. In the case of a stationary monochromatic excitation localized in space, a representation using modes with complex wavevectors is well suited. It corresponds to a dispersion relation with backbending. is simple analysis yields a simple prescription to 1.3. General íeld representations 13 F 1.3 – A point-like dipole located nearby the dielectric-metal interface choose the proper dispersion relation. Note that in the case of pulses limited in space, both representations can be used.