CONTROL OF FWT EQUIPPED BY A PERMANENT MAGNET SYNCHRONOUS GENERATOR

CONTROL OF FWT EQUIPPED BY A PERMANENT MAGNET SYNCHRONOUS GENERATOR

In Chapter 2, several adaptive high order sliding mode control algorithms have been applied on the FWT in Region III. Thanks to these novel approaches, both the power variation and the platform pitch motion are compared with the GSPI controller (J. Jonkman 2008b). These results have been obtained based on the fact that the generator torque is supposed to be fixed at its rated value, the power regulation being achieved by the rotor speed regulation. In fact, no model and control of electrical generator is considered. by a PMSG. The control is not only acting on the aero/hydrodynamic part, but also considers the electrical part that has not been made in previous chapter. Hence, both the collective blade pitch control and the generator torque control are now considered. In the sequel, the reference generator torque is no longer constant at the rated value, but is now varying with the rotor speed in order to guarantee a better regulation of power. The reference rotor speed is varying with platform pitch velocity as perennially to ensure attenuation of the platform pitch motion. Moreover, since a gen- erator is considered, the limitation of oscillations of the electromagnetic torque is also taken in to consideration. In summary, the main contributions of this chapter are:

The PMSG is used by an industrial way, since it has features of high efficiency, high reliability, and low maintenance level (Haque, Negnevitsky, and Muttaqi 2010; Benelghali, Benbouzid, and Charpentier 2012; Keysan, McDonald, and Mueller 2011). Those features appear to be especially suitable for the wind turbines power generation systems, and the synchronous generator plays a crucial role in transforming mechanical energy into electrical energy. The mathematical model of the synchronous generator is a prerequisite in order to design the control algorithms. In this section, models of the PMSG in both the three-phase plane and the rotary d−q reference frame, are recalled. The expressions of PMSG model in the three-phase reference frame are not easy to manipulate and for the control design. The three-phase-two-phase transformation makes it possible to obtain a simplified representation of the PMSG in a plane equivalent to two axes. By using the so-called Park’s transformations (Park 1929; Vas 1998), the a, b, c three-phase currents of the stator are transferred to the direct axis (d-axis), quadrature axis (q-axis) and the zero axis (0-axis) perpendicular to the d − q plane along with the rotor rotation, thus simplifying the analysis of synchronous machine. The standard model of PMSG in the d − q frame reads as

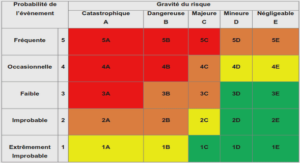
to avoid overload operation and protect the electric machine; the second objective consists in attenuating the platform pitch motion so as to protect mechanical structure. In Chapter 2, the power regulation is achieved by regulating the rotor speed Ω These two approaches will be used in the sequel. It has been demonstrated that, for the baseline GSPI control, the constant power strategy results in a smaller power variation (obvious given that the power is directly controlled) but induces additional platform pitch motion and structure loads whereas the constant torque strategy increases power variation but gives better performances on platform pitch motion and structure loads (Larsen and Hanson 2007; J. Jonkman 2008a; H. Namik and K. Stol 2014)., and then acting on the power output. Hence, according to the two control approaches (constant torque (3.17) and constant power (3.18)), the desired quadratic current ito zero (Glumineau and De León-Morales 2015; Z. Chen 2013). The reference of this current is given by The simulations have been carried out assuming that the FAST 5MW OC3-Hywind floating wind turbine model is equipped with a permanent magnet synchronous generator. The parameters of the PMSG are displayed in Table 3.1 and the characteristics of the FWT have been detailed in Chapter 1. All simulations are made by co-simulation between all DOFs enabled FAST model and SIMULINK, the simulation time being 600 seconds. Euler integration algorithm is used with a fixed step of 0.0125 second. Four control strategies based on the control input defined by (3.39) are pre- sented and compared in the sequel