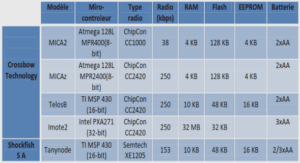
Solution characterization for relaxed constraint satisfaction problems

Solution characterization for relaxed constraint satisfaction problems

This chapter presents several methods to represent the solution of a relaxed constraint satisfaction problem or relaxed CSP (See de.nition 2.2). A relaxed CSP can usually be represented by a set of equations (also called constraints) which involve an unknown variable to be determined. This variable belongs to a particular set called domain or search space. In this chapter we try to characterize the elements of the search space which satisfy only a part of the constraints. The .rst method introduced in [Jaulin, 2009] consists on searching for the set of elements satisfying at least a speci.c number of constraints. This method is explained in section 2.4. The second method to deal with the relaxed CSPs can be seen as an extension of the pre- vious method. The degree of satisfaction of an element of the search space is the number of constraints it satis.es. Instead on focusing on the set of elements having a particular degree of satisfaction, the idea is to consider all the sets for all degrees of satisfaction. The contribution here is to consider a polynomial with set valued coe¢cients which coe¢cients are those sets. The degree of each coe¢cient corresponds to the degree of satisfaction of the elements in that set coe¢cient. The choice of polynomial notation allow to take be- ne.t from the polynomial arithmetics. The .rst bene.t is a simple representation of the solution of the relaxed CSP in the form of a product of monomials. The second bene.t is the possibility represent the solution of a distributed relaxed CSP. A relaxed CSP is dis- tributed when the constraints are not immediately available at the same time and place.

A lattice is a partially ordered set closed under least upper and greatest lower bounds (see [Davey and Priestley, 2002], for more details). The set of all subsets of Rn has a lattice structure. As such, the concept of set polynomials is generalized to lattice polynomials where the coe¢cient belong to a lattice. The lattice polynomials are explained in section 2.5. This chapter introduces another representation of the solution of a relaxed CSP in the form of a function called accumulator. For each element, the accumulator function re- turns the degree of satisfaction of that element (number of constraints it satis.es). The characteristic function of a set is the function returning 1 for elements belonging to that set and 0 otherwise. The accumulator provides a simple representation of the solution of the relaxed CSP is the form of a sum of the characteristic functions of the set as- sociated to the constraints in the relaxed CSP. The accumulators can also be used to represent the solution of distributed relaxed CSPs. The accumulator theory is close to fuzzy logic [Klir and Yuan, 1995] [Nguyen and Walker, 2005] [Zadeh, 1965] and the gen- eralized Hough transform [Bovik, 2000]. This link is also explained in this chapter. The accumulators are explained in Section 2.6.

Extended summary

This section explains the di¤erent approaches to represent the solution of a relaxed CSP in a shortened form highlighting the most important results. Reading this section is not necessary to understand the latter part of the manuscript. The purpose is for the reader to be able to see the whole theory in a condensed form without being lost in the details. Each time a result is presented, a reference to the section and subsection where the result is explained in more details is provided. Consider the following relaxed CSP fi : Rm ! Rpi Ci : fi(x) 2 [yi]; x 2 [x]; [yi] 2 IRpi ; i 2 f1; ::; ng: (2.4) In order to solve this problem, the .rst method introduced in [Jaulin, 2009] consists on searching for the set Sq of elements satisfying all of the constraints fC1; ::;Cng relaxing q 2 f1; ::; ng of them. This means that up to q constraints can be not satis.ed or inconsistent. This also means that Sq is also the set of points which satisfy at least n 􀀀 q constraints. Note that there is an equivalence between the formulations « relaxing q constraints » and « satisfying n􀀀q constraints ». The .rst one is usually used when the number of constraints to be relaxed (or inconsistent constraints) is low. Such is the case of the localization problem, which can be set into a relaxed CSP, where the inconsistent constraints are caused by outliers in sensor data with a ratio inferior to 30%.

The set Sq is de.ned by Sq = fx 2 [x]; 9K _ f1; ::; ng; card(K) =n 􀀀 q; 8i 2 K; fi(x) 2 [yi]; [yi] 2 IRpig: (2.5) Denote by Xi the set of elements satisfying the constraint Ci Xi = fx 2 Rm; fi(x) 2 [yi]g; [yi] 2 IRpi ; i 2 f1; ::; ng: (2.6) The sets Xi play an important role in the characterization of the di¤erent solutions of the relaxed CSP. For example, the set of point satisfying all the constraints (the solution of the CSP) is the intersection of the Xi sets. As for the solution set Sq of the relaxed CSP assuming q inconsistent constraints is de.ned by the q-relaxed intersection of the Xi sets (See subsection 2.4.3). The q-relaxed intersection of the Xi denoted \fqg i2f1;::;ng Xi is the set of point belonging to at least n 􀀀 q sets among Xi sets. As such Sq = \fqg i2f1;::;ng Xi = fx 2 Rm; 9K _ f1; ::; ng; card(K) =n 􀀀 q; 8i 2 K; x 2 Xig: (2.7) In the case of localization of a robot, the real number of inconsistent constraints qreal is usually unknown and may vary with time. It is sometimes possible to assume a maximum number of inconsistent constraints qmax. We consider Sqmax being the solution of the problem. The solution set Sqmax is a guaranteed solution i.e. the real position is certainly in Sqmax as long as the real number of outliers qreal is lower than qmax. This approach is explained in more detail in section 2.4. Note that, since qreal < qmax, we have Sqreal _ Sqmax which means that the solution set Sqmax is overestimated.

One of the contributions to the PhD thesis was to try to .nd a new representation of the solution of a relaxed CSP and avoid such overestimation. The approach consists on considering all the solution sets Sq for all possible values of q. As such, before coming up with the polynomial representation, the .rst mathematical representation of the solution of a relaxed CSP was in the form of a vector of sets (Sn􀀀1; ::; S0). To characterize this vector we considered a transform denoted T which we called the sort transform such as the vector (Sn􀀀1; ::; S0) is the transform of the vector of sets (X1; ::;Xn) de.ned in 2.6. We have (Sn􀀀1; ::; S0) = T (X1; ::;Xn): (2.8) The sort transform T is actually introduced in subsection 2.5.3. The name of the sort transform comes from the fact that the output vector of sets is sorted with descending order relatively to the _ order i.e. S0 _ ::: _ Sn􀀀1. The sort transform provides a formula for each solution set Sq; q 2 f1; ::; ng which corresponds to the q-relaxed intersection of the Xi; i 2 f1; :; ng sets. The representation of the solution of a relaxed CSP in form of a vector of sets (Sn􀀀1; ::; S0) may seem lacking since each element of the vector Sq is computed separately using the sort transform formula (q-relaxed intersection).

Basically the sort transform doesn.t provide a unique formulation involving all of the Xi; i 2 f1; :; ng sets which allow to obtain the Sq; q 2 f0; ::; n􀀀1g sets. The solution we propose is to use polynomial representation. The idea is to consider polynomials with set valued coe¢cients also called set polynomials. We consider a polynomial called solution set polynomial which coe¢cients are the elements of the vector (Sn􀀀1; ::; S0) such as the degree of the coe¢cient corresponds to the number of constraints which are satis.ed by the elements in that set coe¢cient. Denote by X_(s) this polynomial X_(s) = Xn k=0 Sn􀀀ksk: (2.9) The purpose of using polynomial representation is to take advantage of the set polynomial arithmetics (sum, product) to represent the sort transform with a unique formulation. The product and sum of set polynomials is similar to the product and sum of real polynomials just that the product  » _  » of two coe¢cients is replaced by their intersection  » \  » and the sum « + » of two coe¢cients is replaced by their union « [« . Consider the polynomial Y _(s) = Yn k=1 (Xks + Rm) (2.10) By expanding the polynomial Y _(s) we .nd that

Representing the solution of a relaxed CSP using set polynomials The previous section presented how to compute the solution set Sqmax of a relaxed CSP assuming that the number of inconsistent constraints is always inferior to qmax. In the context of localization, inconsistent constraints comes from outliers in sensor data. It is not easy to know exactly the number of those outliers which may also vary with time. As such, the estimated maximum of inconsistent constraints (in the localization case outliers in the data) qmax may be easily overestimated. In this case, the solution set Sqmax is also overestimated. One of the contributions to the PhD thesis was to try to .nd a new representation of the solution of a relaxed CSP and avoid such overestimation. The approach consists on considering all the solution sets Sq for all possible values of q i.e. the vector of sets (Sn􀀀1; ::; S0). The .rst approach is to consider that this vector of sets is the result of a transform called the sort transform of the vector of sets of elements satisfying one constraint from the relaxed CSP at a time (the Xi sets de.ned in (2.20)).

The sort transform provides a formula for each of the solution sets Sq; q 2 f0; ::; n 􀀀 1g but doesn.t provide a unique formulation of the solution as a whole. The idea is to consider polynomials with set valued coe¢cients also called set polynomials. We consider a polynomial called solution set polynomial which coe¢cients are the elements of the vector (Sn􀀀1; ::; S0) such as the degree of the coe¢cient corresponds to the number of constraints which are satis.ed by the elements in that set coe¢cient. The purpose of using polynomial representation is to take advantage of the set polynomial arithmetics (sum, product) to represent the sort transform with a unique formulation as a product of monomials. Because the set of all subsets of Rm has lattice structure, all the theory is generalized to lattices. Lattices are de.ned in subsection 2.5.2. The sort transform of vectors de.ned on lattices is de.ned in subsection 2.5.3. Lattice polynomials i.e. polynomials with lattice valued coe¢cients are de.ned in subsection 2.5.4. The use of set polynomials to represent the solution of a relaxed CSP is de.ned in subsection 2.5.5. Another advantage of the polynomial representation is to represent the possibility of distributed computations of a relaxed CSP. This concept is presented in subsection 2.5.6. Set polynomials based solvers are implemented in section 5.1 of chapter 5.