The impact of antenna switching time on spatial modulation

Spatial modulation (SM) is an antenna-transition-based scheme that has been developed in the last decade Mesleh et al. (2008); Jeganathan et al. (2008b) with unique features. Data rate increment achieved via the utilization of the index of actively transmitting antenna is the core of this modulation scheme. Other benefits of using such modulation schemes comprise improved capacity, spectral and energy efficiency, the reduction to a single RF chain and the removal of inter-channel interference and inter-antenna synchronization requirements. Despite the existence of some drawbacks in this system like the absolute reliance of its performance on channel state information (CSI), i.e. being sensitive to channel correlation and erroneous CSI Soujeri & Kaddoum (2015), it has been the focus of many research studies in the last decade. While bit error rate (BER) performance evaluation has received most attention, very little has been discussed about antenna transitions that constitute a critical property of SM systems. In fact, a study of MIMO antennas for mobile handsets has been carried out in Shoaib et al. (2015) where the isolation properties of decoupling mechanism of certain antennas are discussed. In this regard, parasitic antennas which rely on Micro Electro Mechanical Systems (MEMS) technology for RF applications are already being used in handheld mobile devices. Further, the switching time in MEMS technology is known to be in the range of 2 − 50μs which renders it inefficient for today’s high-speed applications. Indeed, since SM may require a transition (switching) to happen for the transmission of each individual symbol to materialize, it is clear that switching times in antenna controllers must be significantly smaller than the symbol period. This requirement puts the option of MEMS-based switching technology off the table. According to Kalis et al. (2014), parasitic antenna arrays for MIMO applications using semiconductor diodes faster than 0.1μs (100 ns) are available. While in Ishibashi & Sugiura (2014), the effects of antenna switching on band-limited spatial modulation is investigated, where the employment of an SM-specific practical time-limited shaping filter is taken into account and the use of multiple RF chains is considered to transmit the side-lobes of bandlimited pulses, in many recent works, i.e. Serafimovski et al. (2013) and Di Renzo et al. (2014), this issue has never been tackled or debated. This work is the first in this regard to shed the light on the feasibility of implementation of SM technology under the speed constraints of currently existing antenna switching technologies.

Contributions
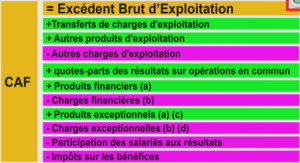
Encouraged by the fact that RF antenna switches constitute an important part of the RF front end Bowick (2011) utilized in SM systems and we admit that these RF switches are neither cost-free nor steeply climbing (in zero-time) and require certain advanced technologies to perform, i.e. acknowledging that switching time intervals introduce systematic transmission gaps in SM systems which overshadow its overall communication performance. In this letter, we calculate the effective data rate, the effective capacity and the spectral efficiency of SM systems for the first time under this practical constraint. In fact, we explore the speed limitations of industrial RF switches to analyse the SM system and to develop expressions for the effective data rate, effective capacity and spectral efficiency. We also identify the upper bound on the switching time interval such that the capacity superiority of SM with respect to single antenna transmission systems is sustained.

Analytical View
In an RF front end, we view the switching time as the time needed for the RF switch to forward an incoming signal to an antenna on one of its branches. In an SM system with Nt antennas at the transmitter, the process of choosing an antenna at every transmission period is a mutually exclusive event that follows a discrete uniform distribution. Since the antenna index is chosen from a constellation, a given antenna, i.e. the kth antenna is chosen with a probability of  Ps = Pr(a = ak) = 1/Nt,    (1.1) .

where Ps denotes the probability that the transmission stays on the kth antenna to transmit the next symbol, i.e. no switching happens. Likewise, the probability of switching to another antenna Psw to transmit the next symbol would become  Psw=1−Ps = 1−1/Nt. (1.2).

Effective SM Capacity
We use the conventional information theory approach Prisecaru (2010) to calculate the capacity of SM systems as   CSM = （ m+nt ) ( 1+ pe log2(pe) + pclog2(pc))bpcu(1.6)

where pe represents the probability of error of SM detection in fading channels, pc = 1− pe is the probability of correct detection and m+nt represents the total number of bits conveyed by the SM system, where m bits choose a constellation symbol and nt bits choose an antenna for transmission. Furthermore, the capacity of SM is not calculated the way it is done for MIMO communications, this is because the calculation of MIMO capacity CMIMO does not apply Prisecaru (2010). In fact, the antenna number in SM represents added information and the antenna pattern is considered as spatial constellation, not as an information source as in MIMO. Moreover, other forms of determining the SM capacity based on mutual information may also be found in An et al. (2015). Note that pe is calculated in a fading channel environment since SM is not defined for AWGN channels in which it is impossible to detect the antenna indices which require the uniqueness of channel coefficients. Ideally, the achievable SM data rate Rs would be Rs ≤ CSM, (1.7)

where Rs = 1/Ts and in practical situations where Tsw = 0, the effective SM data rate would be bounded as Ref ≤ Cef, (1.8)