Privately secure algorithms involving only one trusted party

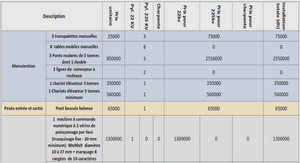
Private and Cheat-free Outsourcing of Algebraic

Computations (Benjamin & Atallah, 2008) Assume that a data owner A has two n×n input matrices A and B and because of his limited computation resources cannot execute more than O(n2) computations nor the expensive public key encryptions of all input values. The goal is obtaining the product matrix AB using two untrusted third parties, let say cloud system S1 and S2, with enough computational resources. As usual, there should not be any information leakage about the input matrices or their product to the cloud systems. Moreover, any malicious behavior of any cloud system should be detectable with high probability by A . The first step of this algorithm is hiding the input matrices. So the owner A generates two random matrices R1 and R2 and computes A = A−R1 and B = B−R2. He also generates two other random matricesU and V and computes their Schur product R=U V – this corresponds to the multiplication of the corresponding pairs of elements (i.e., ui, j ×vi, j). Then, A sends R1, R2 and U to the cloud S1, and A , B and V to the cloud S2. He also sends some temporary public and private keys of a semi-homomorphic cryptographic system to S1.

Now, S1 computes R1R2, EncA (R1), EncA (R2) and EncA (U) and sends them back to A . On his side, S2 computes A B and sends it back to A . Then, A sends the values just received from S1 i.e., R1R2, EncA (R1), EncA (R2) and EncA (R ) to S2. Here, S2 computes EncA (R1B ), Enc(A R2) and EncA (U V) = EncA (R). This can be done due to the homomorphic property of the cryptographic system and the fact that S2 has always the second element in cleartext. Finally, S2 computes and sends back to A the following matrix: EncA (R1B )EncA (A R2)EncA (R) = EncA (R1B +A R2 +R). The owner A sends the received matrix to S1 who decrypts it and send it back in plaintext. A subtracts R and gets R1B +A R2. Finally, he adds this value with the value of A B −R1R2, which has been received previously, to obtain the desired result AB. The above protocol is vulnerable to any malicious behavior of the cloud systems S1 and S2. They can easily return wrong results. By modifying this scheme, A can catch any incorrect result by high probability. He simply needs to generates a random n×1 vector matrix V and computes (AB)V and A(BV), if the equations are equal, the cloud systems are honest with high probability otherwise they did not follow the instructions.

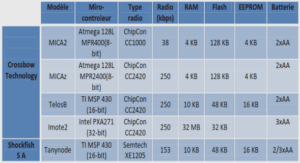
Efficient Secure Outsourcing Computation of Matrix Multiplication in Cloud Computing Zhang et al. (2016) The last solution presented in the chapter is a bit different than the other ones. It has a participant who plays a new role in the solution. It is also based on a different cryptographic paradigm. Three parties are included in this scheme: the data owner A (also referred to as the client of the system), the cloud system and the verification party. It is based on five functions: Key generation, Preprocessing, Requesting, Computation, Verification, Decryption. The system model is shown in Figure 2.8. The new actor has an important role. His task is to verify the correctness of the encrypted computations done by the cloud system. KeyGen: The cloud generates the parameters of bi-linear groups: param=(q,g1,g2,gt ,G1,G2,Gt , e). The cloud publishes param as well as the hash of his secret key SK. This solution is the first one that is not using a semi-homomorphic cryptosystem. It is based on bilinear pairings, which is a powerful concept. It has been used extensively in the past. In this context, only one example is given. Fiore & Gennaro (2012) proposed to use bilinear-pairings to develop a solution for the matrix multiplication allowing an external verifier to check the computations done by a third party.

Security Analysis

The aforementioned algorithm is secure against the semi-honest adversaries. This means that if all the parties follow the algorithm but anyone tries to obtain more information about the initial data or the result, there is no success since the input matrices are either encrypted or randomized using long enough random number or keys. However, we have to consider that the communications with the two trusted parties take place over secure channels (in system communications). Otherwise, the result owner would be able to retrieve easily the matrix A, which is simply encrypted with his own public key. Once this first matrix is known, it can be inverted and the matrix B will be readily obtained from the resulting matrix AB – since A−1(AB) = B). Unfortunately, if there are some collusion among the participants, the different matrices are at risk. In the case of a collusion between T1 and T2, they would obtain easily the matrix B. T2 would need to decrypt the random matrix R and share it with T1. This latter participant would then retrieve easily the values of the matrix B. On the other hand, since all the entries of the matrix A are encrypted with the public key of the result owner O, there will not be any information leakage of this matrix even in case of collusion between the third parties. But if one of them colludes with O, everything falls apart. Just too much information is shared among these malicious participants. Finally, if the result owner O can pretend to be one of the data owners and send some input matrices to the trusted parties, again the all protocol falls apart. For example, if O pretends to own the matrix A and sends it T1, he would be able to retrieve easily the matrix B without any more effort. He would simply send the identity matrix I and would obtain back form T2 the resulting matrix IB = B.

In the real world, designing a privacy-preserving algorithm for mathematical computation is often very complex with the presence of different sorts of adversaries and attackers. In this thesis, we have presented some algorithms for different system models, which satisfy the definitions of a secure algorithm. Each one preserves (partially or totally) the privacy of the information. The applications of the proposed algorithms are big-data mining and analysis. In such cases, the importance of assuring the privacy of the results is crucial. Since the adversaries are usually malicious and have more and more resources, keeping the private information of the clients secure is more and more costly in terms of time and money. However, there should always be a trade-off between the costs and the level of privacy provided by the outsourcing algorithms. Although the proposed algorithms are not fully secure, they can be applied in most of matrix multiplication outsourcing set-ups because the information leakage is mathematically negligible. Moreover, in term of efficiency, we tried to decrease the computation costs on the client side and delegate the most expensive computations to the powerful cloud systems. The only significant computation which should be carry out by the client is the encryption of a matrix which is much cheaper than performing a regular matrix multiplication by himself. Additionally these algorithms avoid the data owners to obtain the product of the matrices which is an important consequence for outsourcing schemes.