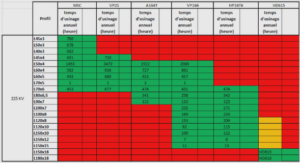
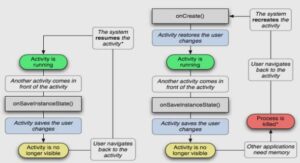
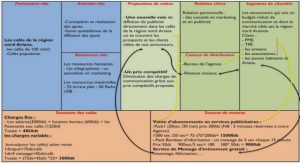
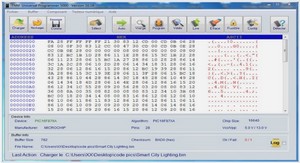
Pour chacune des 20 questions imprimées en gras ci-dessous, on vous propose un certain nombre de réponses. Chaque réponse proposée appelle une réaction de votre part indiquée par Juste (J) ou Faux (F). S.v.p. utilisez le carré au début de chaque réponse. Notez que toutes les réponses proposées pour une question quelconque peuvent être justes, toutes peuvent être fausses ou certaines justes et d’autres fausses. Un carré laissé en blanc sera considéré comme une réaction incorrecte. La note sera déterminée par le pourcentage des réactions correctes, en tenant compte du fait que si vous répondez au hasard vous avez une chance sur deux de tomber juste. Le corrigé de cet examen sera mis sur le site du cours dans les jours qui suivent.
- Lequel des facteurs suivants peut être une source de corrélation sérielle ?
- ! La forme fonctionnelle de l’équation est incorrecte.
- ! La fréquence des « chocs » aléatoires est plus petite que celle des observations.
- ! Le nombre de variables explicatives dépasse le nombre d’observations.
- ! Les variables explicatives sont cycliques.
- Quelles affirmations suivantes sont justes/fausses ?
- ! Les estimations MCO ne sont jamais biaisées par la corrélation sérielle.
- ! La corrélation sérielle est toujours détectée par le d de Durbin-Watson.
- ! L’omission d’une ou plusieurs variables explicatives se traduit toujours par de la corrélation sérielle.
- ! La corrélation sérielle tendra à biaiser les t de Student.
- Parmi les hypothèses suivantes, lesquelles sont des hypothèses de base de la méthode des MCO ?
- ! Le modèle est linéaire dans les paramètres.
- ! Les variables explicatives doivent être strictement orthogonales dans l’échantillon.
- ! Les variables X sont « fixes », c’est-à-dire strictement « sous contrôle ».
- ! Le terme stochastique a une valeur espérée nulle.
- Qu’entend-on lorsqu’on dit que l’estimateur MCO est un « BLUE » ?
- ! L’estimateur est linéaire, non biaisé et non faussé.
- ! L’estimateur est non biaisé et le plus efficient de tous les estimateurs linéaires.
- ! C’est un estimateur « maximum de vraisemblance ».
- ! L’estimateur est efficient et convergent.
- Parmi les tests suivants, lesquels peuvent être utilisés pour détecter la corrélation sérielle ?
- ! Le test d de Durbin-Watson.
- ! Le test Q de Ljung-Box.
- ! Le test F de Fischer.
- ! Le test de stabilité des coefficients par estimations récursives.
- Quels sont les effets d’une variable omise, cyclique et corrélée avec une des variables incluses ?
- ! Le coefficient de la variable incluse est généralement biaisé.
- ! Le test d de Durbin-Watson détecte de la corrélation sérielle « pure ».
- ! La statistiques t du coefficient de la variable incluse est généralement biaisé vers le bas.
- ! La constante estimée ne sera pas significativement différente de zéro.
- Quelle sont les principales limites du test de Durbin-Watson ?
- ! La distribution de la statistique de Durbin-Watson dépend de la distribution des variables explicatives (les X).
- ! Si la variable dépendante retardée figure parmi les variables explicatives, le test de Durbin-Watson n’est plus valide.
- ! Le test de Durbin-Watson teste uniquement l’hypothèse nulle d’absence de corrélation sérielle du premier ordre.
- ! Le test de Durbin-Watson n’est plus valide si la (les) variable(s) explicative(s) est/sont corrélée(s) avec la variable dépendante.
- Quels sont les objets testés par la statistique F ?
- ! Elle teste le degré de colinéarité entre les variables explicatives.
- ! Elle teste l’hypothèse nulle selon laquelle tous les coefficients des variables explicatives du modèle sont conjointement égaux à zéro.
- ! Elle est utilisée dans les modèles de régression simple afin de tester l’hypothèse nulle selon laquelle les résidus de la régression ne sont pas corrélés.
- ! Elle peut être utilisée dans les modèles de régression multiple afin de tester la signification de la statistique du R2.
- Après une transformation de Koyck, on obtient l’équation suivante :
Yt = a(1-w) + bXt + wYt-1 + e*t , avec w = coefficient de « mémoire » et
e*t = et – wet-1
Une équation de ce type soulève les problèmes suivants :
- ! e*t souffrira toujours de corrélation sérielle.
- ! La transformation de Koyck introduit des cycles dans Yt.
- ! e*t n’est pas indépendant de Yt-1 .
- ! Cette équation représente un processus dynamique qui peut ne pas être mesuré correctement si on l’estime par les MCO.