Passage du MCD aux tables relationnelles

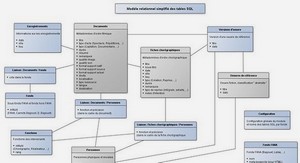
Cours passage du MCD aux tables relationnelles, tutoriel & guide de travaux pratiques en pdf.

L’algebre relationnelle

L’algebre relationnelle a ete introduite par Codd en 1970 pour formaliser les operations sur les ensembles. Il existe deux familles d’operations : les operations ensemblistes et les operations unaires.
Les operations de base
Trouver l’ensemble des operations de base consiste a trouver un ensemble minimal d’operations au sens ou aucune d’entre elles ne peut s’ecrire par combinaison des autres. Il existe plusieurs ensembles minimaux pour l’algebre relationnelle. Celui que nous presentons se base sur 3 operations ensemblistes et 2 operations unaires.
Operations ensemblistes
Les operations ensemblistes de base sont l’union, la di erence et le produit.
L’union de deux relations R et S de m^eme schema est une relation T de m^eme schema contenant l’ensemble des tuples appartenant a R, a S ou aux deux.
On notera T = (R [ S) ou T=union(R,S).
Le produit cartesien de deux relations R et S de schema quelconque est une relation T ayant
pour attributs la concatenation des attributs de R et de S et dont les tuples sont constitues de toutes les concatenations d’un tuple de R a un tuple de S.
On notera T = (R S) ou T=product(R,S)

LES OPERATIONS DE BASE

Operations unaires
Les operations unaires ont pour objectif de permettre l’elimination de colonnes ou de lignes dans la table relationnelle. Ces deux operations sont la projection et la restriction.
La projection d’une relation R de schema (A1; A2; : : : ; An) sur les attributs Ai1 ; Ai2 ; : : : ; Aip
(avec ij 6= ik et p < n) est une relation R0 de schema (Ai1 ; Ai2 ; : : : ; Aip ) dont les tuples sont obtenus par elimination des attributs de R n’appartenant pas a R0 et par suppression des doublons. On notera T = X1;:::;Xn (R) ou T = projX1 ;:::;Xn (R)
La restriction (ou selection) de la relation R par une quali cation Q est une relation R0 de m^eme schema dont les tuples sont ceux de R satisfaisant la quali cation Q.
La quali cation Q peut ^etre exprimee a l’aide de constantes, comparateurs arithmetiques (>
; ; <; ; =; 6=) et operateurs logiques (_; ^; :). On notera T = Q(R) ou T = selectQ(R)
Les cinq operations precedentes (union, di erence, produit, projection, restriction) forment un ensemble coherent et minimal. Aucune d’entre-elles ne peut s’ecrire a l’aide des autres. A partir
de ces cinq operations elementaires, d’autres operations (sans doute plus pratiques) peuvent ^etre de nies.
Operations derivees
Les operations derivees sont construites a partir des cinq operations de base. Nous presentons ici quelques operations additionnelles mais cette liste n’est pas limitative. Bien d’autres pourraient ^etre ajoutees.
L’intersection de deux relations R et S de m^eme schema est une relation T de m^eme schema contenant les tuples appartenant a la fois a R et a S.
On notera T = (R \ S) ou T = inter(R; S).
Remarque : il existe 3 types d’intersection dans la theorie des ensembles. L’intersection entre deux ensembles extensionnels, entre deux ensembles intentionnels et entre un intentionnel et un extensionnel. L’algebre relationnelle n’en code que deux : l’intersection entre deux ensembles exten-sionnels (par l’intersection precedemment de nie) et l’intersection entre un ensemble extensionnel et un ensemble intentionnel (par la restriction avec une quali cation). On ne peut pas faire, par exemple, l’intersection entre l’ensemble des nombres pairs et l’ensemble des multiples de3.
Le quotient (ou division) de la relation R de schema R(A1; A2; : : : ; An) par la sous-relation
S de schema S(Ap+1; :::; An) est la relation T de schema T (A1; A2; Ap) formee de tous les tuples qui concatenes a chaque tuple de S donnent toujours un tuple de R.
On notera T = (R=S) ou T = div(R; S)
Le quotient permet concretement de rechercher l’ensemble de tous les sous-tuples d’une relation satisfaisant une sous-relation decrite par l’operation diviseur. Il permet de chercher \les tuples de R qui veri ent tout les tuples de S. Chercher par exemple tous les produits qui existent dans une gamme de couleurs et/ou une gamme de prix.
La jointure de deux relations R et S selon une quali cation Q est l’ensemble des tuples du produit cartesien R S satisfaisant la quali cation Q.

1 Presentation generale 
1.1 Qu’est ce qu’une base de donnees
1.2 Objectifs et avantages
1.3 Dierents types de bases de donnees
1.4 Quelques systemes existants
1.5 Les niveaux ANSI/SPARC
1.6 Modeliser les donnees
1.7 Exemple de MCD
1.8 Le modele relationnel
1.9 Exemple de base de donnees relationnelle
1.10 Passage du MCD aux tables relationnelles
2 Presentation des donnees 
2.1 Les formulaires
2.2 Les etats
3 L’algebre relationnelle 
3.1 Les operations de base
3.2 Operations derivees
3.3 Les operations de calcul
3.4 Expressions de l’algebre relationnelle
3.5 Quelques remarques sur l’algebre relationnelle
4 Les contraintes d’integrite 
4.1 Contraintes de cle
4.2 Contraintes de types de donnees
4.3 Contraintes d’integrite referentielle
5 Le langage QBE 
6 Le langage SQL 
6.1 La manipulation des donnees : le DML
6.2 La denition des donnees : Le DDL
6.3 L’aspect multi-utilisateurs : le DCL
6.4 Le catalogue
7 SQL Integre 
7.1 Liens entre SQL et le langage applicatif
7.2 Exemple de programme SQL Integre
7.3 Programme COBOL
7.4 Programme VBA sous ACCESS
8 La gestion des transactions 
8.1 La tolerance aux pannes
8.2 L’acces concurrent aux donnees
9 Normalisation des Relations 
9.1 Le besoin de Normalisation
9.2 La Premiere Forme Normale
9.3 Notion de dependance fonctionnelle: DF
9.4 Decomposition d’une relation en sous-relations
9.5 La Deuxieme Forme Normale
9.6 Troisieme Forme Normale
9.7 La Troisieme Forme Normale de Boyce-Codd
9.8 Methodologie
9.9 Les Dependances Multivaluees
9.10 Les Dependances Hiearchiques
9.11 Conclusion sur la Normalisation
10 Les bases de donnees de type reseau
10.1 Notions de base
10.2 Le SGBD de type CODASYL IDS-II (Integrated Data Store)
10.3 Utilisation
10.4 Avantages et inconvenients des bases de donnees de type reseau
11 Le mode Client-Serveur 
11.1 ODBC
11.2 JDBC
11.3 WEB et Bases de donnees
12 Les serveurs d’applications 
12.1 Le suivi de session
12.2 Les Java Server Pages : JSP
12.3 Les serveurs d’applications