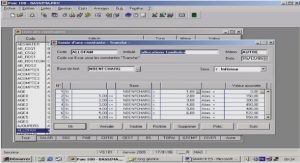
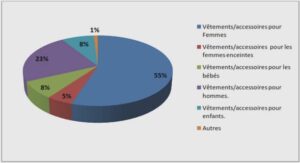
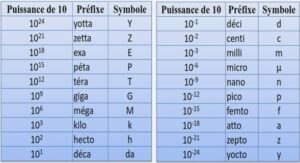
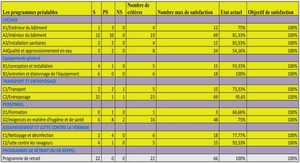
Probabilité exercices corrigés, tutoriel & guide de travaux pratiques en pdf.
THÉORIE DE LA MESURE
Énoncés
1.1 Soit E une partie (fixée) d’un ensemble R, et soit &=(A€P(R): ACE}
Déterminer l’algèbre de Boole engendrée par 1.
1.2 Si Al et A2 sont des tribus sur R? on pose
Démontrer que a(J) = a(A1 U Az) = o(U).
1.3 Soit (R = R1 x R2,A = A1 @ A2) un espace mesuré produit. Si A E A, montrer que pour tout w1 E 01, la section A,, = { w2 E 02 : (w1, w2) E A } est mesurable.
1.4 Soit (fn)ntN une suite de fonctions mesurables de (0,A) dans un espace métrique (E,d) muni de sa tribu borélienne. On suppose que fn converge ponc- tuellement vers f (i.e. pour tout w E R, limn-ocjfTL(w) = f(w)). Montrer que f est mesurable. Indlctrttorr : pour fout ouil( rt Ir dr E ( f I’ E W torricdr:r( I U, = { I’ E U : (/(I. I-; \ IT) > il1 1. 17c7/fipr f-l(r;) = u, 111 nli>ll, j,;~(v,).
CHAPITRE I. THI~ORIE DE LA AIESURE
1.5 Si x = (21,. . . ,xn) E IRn, on note +(x) le vecteur x ordonné par ordre croissant, i.e. dans le cas où tous les x2 sont distincts, on a +(x) = (XI,,, . . . , xn,,), où XI,, = min1121n x, et x,,,=min({x, : i<z<n}\{xJ,, : i<j<z-1}), 25i~n. Montrer que + est mesurable. Indiccit~oii tout 1 5 2 5 71 mi considirant IC 3 c.nsrrrili7e~ { I I ,, 5 (I }. (I E R. or1 poirrrci conirrifr1(cr par rrrmtrci qiic I t-) r ,) cst rnr~surablt~ pour
1.6 Sur IR on définit la relation d’équivalence z N y si 2 – y E Q. En utilisant l’axiome du choix (si A est une fonction sur un ensemble I telle que A(x) # 0 pour tout x de I, il existe une fonction f telle que f(x) E A(x) pour tout x E I), construire un ensemble A C [O, 1 [ qui contient exactement un point de chaque classe d’équivalence. Supposons A mesurable, et soit a = X(A) sa mesure de Lebesgue. Montrer que si T,S E Q et T # s, alors (A + s) ri (A + r) = 0, où A + x = {y + x : y E A}, et que X(A + s) = X(A). Remarquer que Un exemple d’ensemble non mesurable. 1 = X([0,1]) I X( u (A+T)) I X([-1,2]) =3.
En utilisant la 0-additivité de A, montrer que cette inégalité conduit d’une part à a = O, d’autre part à a > O. Conclure. ram] -1,1[
1.7 Théorème d’Egorov. Soit (Q, A, p) un espace mesuré tel que p(R) < 00 ; on considère des applications f, f,, n E N, de R dans IR, telles que f, + f p-p.p., c’est-à-dire, telles que P({W : fn(4 74 f(4 >) = 0. a) Pour n E N et E > O, soit G,,, = {w E R : Ifn(w) – f(w)l 2 E} et E,,, = Urn>, Gm,E. Démontrer que pour tout E > O,
et en déduire que limn+m p(E,,+) = O.
11) Déduire de la question précédente que pour tous ~,b > O, il existe no E N et BE,6 E A tels que p(B,,b) < 6 et pour tout w E R \ BE,6 et tout n 2 no, IfnW – f(4 5 E.
c) Soit a > O ; pour tout entier p 2 1, on pose E, = l/p, 6, = a/2p, A, = BEp,b, et A = Up>i A,. Démontrer que p(A) 5 a et que fn + f uniformément sur O\A.
1.8 Soit (0, A, p) un espace mesuré. Une partie N C R est dite pu-négligeables i elle est contenue dans un ensemble mesurable A tel que p(A) = O. La tribu B est dite complète pour p si elle contient’ tous les ensembles négligeables. Si N désigne l’ensemble des parties p-négligeables, soit
,A,= {AuN; AEA, NEN}.
Montrer que A, est une tribu, appelée la tribu p-complétée de A.
1.9 Soient X et Y deux espaces topologiques munis respectivement des tribus boréliennes Bx et By, p une mesure sur Bx, et f : X -f Y une fonction continue p-p.p., c’est-à-dire telle que l’ensemble N = { z E X : f discontinue en x} soit p-négligeable. Démontrer que f est mesurable de (X, Bx) dans (Y, By) où ax est la tribu complétée de Bx par rapport à p.